
题目列表(包括答案和解析)
(本小题满分14分)
已知定点A(1,0)和定直线x=-1的两个动点E、F,满足AE⊥AF,动点P满足EP∥OA,FO∥OP(其中O为坐标原点).
(1)求动点P的轨迹C的方程;
(2)过点B(0,2)的直线l与(1)中轨迹C相交于两个不同的点M、N,若∠MAN为钝角,求直线l的斜率的取值范围;
(3)过点T(-1,0)作直线m与(1)中的轨迹C交于两点G、H,问在x轴上是否存在一点D,使△DGH为等边三角形;若存在,试求出点D的坐标;若不存在,请说明理由.
(本小题满分14分)已知定义在实数集上的函数fn(x)=xn,n∈N*,其导函数记为 ,且满足
,且满足
 ,a,x1,x2为常数,x1≠x2.
,a,x1,x2为常数,x1≠x2.
(1)试求a的值;
(2)记函数
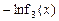 ,x∈(0,e],若F(x)的最小值为6,求实数b的值;
,x∈(0,e],若F(x)的最小值为6,求实数b的值;
(3)对于(2)中的b,设函数 ,A(x1,y1),B(x2,y2)(x1<x2)是函数g(x)图象上两点,若
,A(x1,y1),B(x2,y2)(x1<x2)是函数g(x)图象上两点,若 ,试判断x0,x1,x2的大小,并加以证明.
,试判断x0,x1,x2的大小,并加以证明.
(本小题满分14分)已知定义在实数集上的函数fn(x)=xn,n∈N*,其导函数记为 ,且满足
,且满足
 ,a,x1,x2为常数,x1≠x2.
,a,x1,x2为常数,x1≠x2.
(1)试求a的值;
(2)记函数
 ,x∈(0,e],若F(x)的最小值为6,求实数b的值;
,x∈(0,e],若F(x)的最小值为6,求实数b的值;
(3)对于(2)中的b,设函数 ,A(x1,y1),B(x2,y2)(x1<x2)是函数g(x)图象上两点,若
,A(x1,y1),B(x2,y2)(x1<x2)是函数g(x)图象上两点,若 ,试判断x0,x1,x2的大小,并加以证明.
,试判断x0,x1,x2的大小,并加以证明.
 ,且满足
,且满足
 ,a,x1,x2为常数,x1≠x2.
,a,x1,x2为常数,x1≠x2.
 ,x∈(0,e],若F(x)的最小值为6,求实数b的值;
,x∈(0,e],若F(x)的最小值为6,求实数b的值;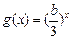 ,A(x1,y1),B(x2,y2)(x1<x2)是函数g(x)图象上两点,若
,A(x1,y1),B(x2,y2)(x1<x2)是函数g(x)图象上两点,若 ,试判断x0,x1,x2的大小,并加以证明.
,试判断x0,x1,x2的大小,并加以证明.(本小题满分14分)
已知直线l与椭圆![]() (a>b>0)相交于不同两点A、B,
(a>b>0)相交于不同两点A、B,![]() ,且
,且![]() ,以M为焦点,以椭圆的右准线为相应准线的双曲线与直线l相交于N(4,
,以M为焦点,以椭圆的右准线为相应准线的双曲线与直线l相交于N(4,![]() 1). (I)求椭圆的离心率
1). (I)求椭圆的离心率![]() ; (II)设双曲线的离心率为
; (II)设双曲线的离心率为![]() ,记
,记![]() ,求
,求![]() 的解析式,并求其定义域和值域.
的解析式,并求其定义域和值域.
一、选择题:
1.C 2.D 3.D 4.C 5. B 6.C 7. C 8.C 9. A
|