
题目列表(包括答案和解析)
| ||
| 2 |
| ||
| 2 |
已知椭圆的中心在坐标原点O,焦点在![]() 轴上,离心率为
轴上,离心率为![]() ,坐标原点
,坐标原点![]() 到过右焦点F且斜率为1的直线的距离为
到过右焦点F且斜率为1的直线的距离为![]() 。
。
(1)求椭圆的方程;
(2)设过右焦点F且与坐标轴不垂直的直线![]() 交椭圆于P、Q两点,在线段
交椭圆于P、Q两点,在线段![]() 上是否存在点
上是否存在点![]() ,使得以
,使得以![]() 为邻边的平行四边形是菱形?若存在,求出
为邻边的平行四边形是菱形?若存在,求出![]() 的取值范围;若不存在,请说明理由。
的取值范围;若不存在,请说明理由。
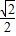 ,坐标原点O到过右焦点F且斜率为1的直线的距离为
,坐标原点O到过右焦点F且斜率为1的直线的距离为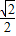 .
.| 1 |
| 20 |
| 1 |
| 4 |
| 1 |
| 25 |
| x2 |
| 2 |
| y2 |
| a |
| OR |
| OS |
已知直线l的方程为![]() ,且直线l与x轴交于点M,圆
,且直线l与x轴交于点M,圆![]() 与x轴交于
与x轴交于![]() 两点(如图).
两点(如图).
(I)过M点的直线![]() 交圆于
交圆于![]() 两点,且圆孤
两点,且圆孤![]() 恰为圆周的
恰为圆周的![]() ,求直线
,求直线![]() 的方程;
的方程;
(II)求以l为准线,中心在原点,且与圆O恰有两个公共点的椭圆方程;

(III)过M点的圆的切线![]() 交(II)中的一个椭圆于
交(II)中的一个椭圆于![]() 两点,其中
两点,其中![]() 两点在x轴上方,求线段CD的长.
两点在x轴上方,求线段CD的长.
一.选择题 1-5 6-10 11-12 BCDCA DADBC AC
二.填空题 13.  ; 14.
; 14.  ;
15.
;
15.  ;
;
16. 
三、解答题
17.【解】(Ⅰ)由 整理得
整理得 ,
,
即 ,------2分
,------2分
∴ , -------5分
, -------5分
∵ ,∴
,∴ 。
-------7分
。
-------7分
【解】(Ⅱ)∵ ,∴最长边为
,∴最长边为 ,
--------8分
,
--------8分
∵
 ,∴
,∴ ,
--------10分
,
--------10分
∴ 为最小边,由余弦定理得
为最小边,由余弦定理得 ,解得
,解得 ,
,
∴ ,即最小边长为1
--------12分
,即最小边长为1
--------12分
18.【解】(Ⅰ)∵ ,∴
,∴ .---2分
.---2分
令 ,得
,得 ,
,
∵ ,∴
,∴ ,即
,即 ,∴
,∴ ,------4分
,------4分
当 时,
时, ,
, 的单调递增区间为
的单调递增区间为 ;------5分
;------5分
当 时,
时, .------6分
.------6分
 的单调递减区间为
的单调递减区间为 和
和 .------7分
.------7分
(Ⅱ)∵ 时,
时, ;------8分
;------8分
 时,
时, ;
; 时,
时, ,------9分
,------9分
∴ 处取得极大值-7. ------10分
处取得极大值-7. ------10分
即 ,解得
,解得 .------12分
.------12分
19.【解】(Ⅰ)由茎叶图可求出10次记录下的有记号的红鲫鱼与中国金鱼数目的平均数均为20,故可认为池塘中的红鲫鱼与中国金鱼的数目相同,设池塘中两种鱼的总数是 ,则有
,则有
 ,
------------3分
,
------------3分
即  ,
,
所以,可估计水库中的红鲫鱼与中国金鱼的数量均为25000. ------------6分
(Ⅱ)从上述对总体的估计数据获知,从池塘随机捕出1只鱼,它是中国金鱼的概率为 .随机地从池塘逐只有放回地捕出5只鱼,5只鱼都是红鲫鱼的概率是
.随机地从池塘逐只有放回地捕出5只鱼,5只鱼都是红鲫鱼的概率是 ,所以其中至少有一只中国金鱼的概率
,所以其中至少有一只中国金鱼的概率 .------12分
.------12分
20.【解】在 中,
中, ,
, ,∴
,∴ .
.
∵ ,∴四边形
,∴四边形 为正方形.
为正方形.
 ----6分
----6分
(Ⅱ)当点 为棱
为棱 的中点时,
的中点时, 平面
平面 .
------8分
.
------8分
 证明如下:
证明如下:
如图,取 的中点
的中点 ,连
,连 、
、 、
、 ,
,
∵ 、
、 、
、 分别为
分别为 、
、 、
、 的中点,
的中点,
∴ .
.
∵ 平面
平面 ,
, 平面
平面 ,
,
∴ 平面
平面 . ------10分
. ------10分
同理可证 平面
平面 .
.
∵ ,
,
∴平面
 平面
平面 .
.
∵ 平面
平面 ,∴
,∴ 平面
平面 . ------12分
. ------12分
21.【解】(Ⅰ)法1:依题意显然 的斜率存在,可设直线
的斜率存在,可设直线 的方程为
的方程为 ,
,
整理得  . ① ---------------------2分
. ① ---------------------2分
设 是方程①的两个不同的根,
是方程①的两个不同的根,
∴ , ②
----------------4分
, ②
----------------4分
且 ,由
,由 是线段
是线段 的中点,得
的中点,得
 ,∴
,∴ .
.
解得 ,这个值满足②式,
,这个值满足②式,
于是,直线 的方程为
的方程为 ,即
,即 --------------6分
--------------6分
法2:设 ,
, ,则有
,则有
 --------2分
--------2分
依题意, ,∴
,∴ .
---------------------4分
.
---------------------4分
∵ 是
是 的中点,
∴
的中点,
∴ ,
, ,从而
,从而 .
.
直线 的方程为
的方程为 ,即
,即 . ----------------6分
. ----------------6分
(Ⅱ)∵ 垂直平分
垂直平分 ,∴直线
,∴直线 的方程为
的方程为 ,即
,即 ,
,
代入椭圆方程,整理得 . ③
---------------8分
. ③
---------------8分
又设 ,
, 的中点为
的中点为 ,则
,则 是方程③的两根,
是方程③的两根,
∴ ,
, .-----10分
.-----10分
 到直线
到直线 的距离
的距离 ,故所求的以线段
,故所求的以线段 的中点
的中点 为圆心且与直线
为圆心且与直线 相切的圆的方程为:
相切的圆的方程为: .-----------12分
.-----------12分
22.【解】(Ⅰ)由 求导得
求导得 ,
,
∴曲线 :
: 在点
在点 处的切线方程为
处的切线方程为 ,即
,即 .
.
此切线与 轴的交点
轴的交点 的坐标为
的坐标为 ,
,
∴点 的坐标为
的坐标为 .即
.即 .
-------------------2分
.
-------------------2分
∵点 的坐标为
的坐标为 (
( ),
), 在曲线
在曲线 上,所以
上,所以 ,
,
∴曲线 :
: 在点
在点
 处的切线方程为
处的切线方程为 ---4分
---4分
令 ,得点
,得点 的横坐标为
的横坐标为 .
.
∴数列 是以2为首项,2为公比的等比数列.
是以2为首项,2为公比的等比数列.
∴ (
( ).
------------------6分
).
------------------6分
(Ⅱ)∵ ;
; ,
,


∴
 .---------10分
.---------10分
(Ⅲ)因为 ,所以
,所以 ,
,
所以数列 的前n项和
的前n项和 的前n项和为
的前n项和为 ①,
①,
---------12分

 ②,
②,
①―②得


 ,
,
所以 ---------14分
---------14分
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com