
题目列表(包括答案和解析)
如图所示,将一矩形花坛ABCD扩建成一个更大的矩形花园AMPN,要求B在AM上,D在AN上,且对角线MN过C点,|AB|=3米,|AD|=2米,
(I)要使矩形AMPN的面积大于32平方米,则AN的长应在什么范围内?
(II)当AN的长度是多少时,矩形AMPN的面积最小?并求出最小面积.
(Ⅲ)若AN的长度不少于6米,则当AN的长度是多少时,矩形AMPN的面积最小?并求出最小面积.

【解析】本题主要考查函数的应用,导数及均值不等式的应用等,考查学生分析问题和解决问题的能力 第一问要利用相似比得到结论。
(I)由SAMPN > 32 得 > 32 ,
> 32 ,
∵x >2,∴ ,即(3x-8)(x-8)> 0
,即(3x-8)(x-8)> 0
∴2<X<8/3,即AN长的取值范围是(2,8/3)或(8,+ )
)
第二问, 
当且仅当
(3)令
∴当x
> 4,y′> 0,即函数y= 在(4,+∞)上单调递增,∴函数y=
在(4,+∞)上单调递增,∴函数y= 在[6,+∞]上也单调递增.
在[6,+∞]上也单调递增.
∴当x=6时y= 取得最小值,即SAMPN取得最小值27(平方米).
取得最小值,即SAMPN取得最小值27(平方米).
某沿海地区养殖的一种特色海鲜上市时间仅能持续5个月,预测上市初期和后期会因供应不足使价格呈持续上涨态势,而中期又将出现供大于求使价格连续下跌.现有三种价格模拟函数:①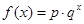 ;②
;②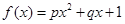 ;③
;③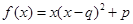 .(以上三式中、
.(以上三式中、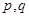 均为常数,且
均为常数,且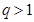 )
)
(I)为准确研究其价格走势,应选哪种价格模拟函数(不必说明理由)
(II)若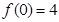 ,
, ,求出所选函数
,求出所选函数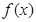 的解析式(注:函数定义域是
的解析式(注:函数定义域是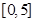 .其中
.其中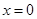 表示8月1日,
表示8月1日,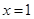 表示9月1日,…,以此类推);
表示9月1日,…,以此类推);
(III)在(II)的条件下研究下面课题:为保证养殖户的经济效益,当地政府计划在价格下跌期间积极拓宽外销,请你预测该海鲜将在哪几个月份内价格下跌.
某沿海地区养殖的一种特色海鲜上市时间仅能持续5个月,预测上市初期和后期会因供应不足使价格呈持续上涨态势,而中期又将出现供大于求使价格连续下跌.现有三种价格模拟函数:①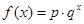 ;②
;②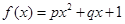 ;③
;③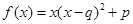 .(以上三式中、
.(以上三式中、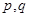 均为常数,且
均为常数,且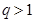 )
)
(I)为准确研究其价格走势,应选哪种价格模拟函数(不必说明理由)
(II)若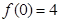 ,
,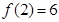 ,求出所选函数
,求出所选函数 的解析式(注:函数定义域是
的解析式(注:函数定义域是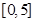 .其中
.其中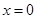 表示8月1日,
表示8月1日,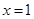 表示9月1日,…,以此类推);
表示9月1日,…,以此类推);
(III)在(II)的条件下研究下面课题:为保证养殖户的经济效益,当地政府计划在价格下跌期间积极拓宽外销,请你预测该海鲜将在哪几个月份内价格下跌.
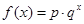 ;②
;②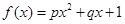 ;③
;③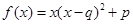 .(以上三式中、
.(以上三式中、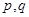 均为常数,且
均为常数,且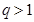 )
)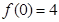 ,
,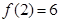 ,求出所选函数
,求出所选函数 的解析式(注:函数定义域是
的解析式(注:函数定义域是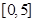 .其中
.其中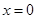 表示8月1日,
表示8月1日,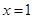 表示9月1日,…,以此类推);
表示9月1日,…,以此类推);某花店每天以每枝5元的价格从农场购进若干枝玫瑰花,然后以每枝10元的价格出售。如果当天卖不完,剩下的玫瑰花做垃圾处理。
(Ⅰ)若花店一天购进17枝玫瑰花,求当天的利润y(单位:元)关于当天需求量n(单位:枝,n∈N)的函数解析式。
(Ⅱ)花店记录了100天玫瑰花的日需求量(单位:枝),整理得下表:
|
日需求量n |
14 |
15 |
16 |
17 |
18 |
19 |
20 |
|
频数 |
10 |
20 |
16 |
16 |
15 |
13 |
10 |
(i)假设花店在这100天内每天购进17枝玫瑰花,求这100天的日利润(单位:元)的平均数;
(ii)若花店一天购进17枝玫瑰花,以100天记录的各需求量的频率作为各需求量发生的概率,求当天的利润不少于75元的概率.
【命题意图】本题主要考查给出样本频数分别表求样本的均值、将频率做概率求互斥事件的和概率,是简单题.
【解析】(Ⅰ)当日需求量 时,利润
时,利润 =85;
=85;
当日需求量 时,利润
时,利润 ,
,
∴ 关于
关于 的解析式为
的解析式为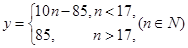 ;
;
(Ⅱ)(i)这100天中有10天的日利润为55元,20天的日利润为65元,16天的日利润为75元,54天的日利润为85元,所以这100天的平均利润为
 =76.4;
=76.4;
(ii)利润不低于75元当且仅当日需求不少于16枝,故当天的利润不少于75元的概率为

一、选择题
题号
1
2
3
4
5
6
7
8
9
10
11
12
答案
A
D
C
C
B
B
A
B
C
D
C
D
二、填空题
13.2 14.-1 15.60 16.③④
三、解答题
17.解:(1)∵ ,
, ,
,
∴ .
…………2分
.
…………2分
又 ,
…………4分
,
…………4分
∴ ,∴
,∴ .…………5分
.…………5分
(2)∵ ,
, ,
, ,
,
∴ .
…………7分
.
…………7分
∵ ,
,
∴ . …………9分
. …………9分
 ∴
∴ ,
,
∴ .…………10分
.…………10分
18. (1)证明:连结BD交AC于点M,取BE的中点N,
连结MN,则MN∥ED且MN= ED,依题意,
ED,依题意,
知AG∥ED且AG= ED,
ED,
∴MN∥AG且MN=AG.
故四边形MNAG是平行四边形,
AM∥GN,即AC∥GN,…………4分
又∵ ,
,
∴ AC∥平面GBE. …………6分
(2)延长EG交DA的延长线于H点,
连结BH,作AP⊥BH于P点,连结GP.
∵ 平面ABCD⊥平面ADEF,平面ABCD∩平面ADEF=AD ,
GH 平面ADEF, GA⊥AD.
平面ADEF, GA⊥AD.
∴ GA⊥平面ABCD,由三垂线定理,知GP⊥BH,
故∠GPA就是所求二面角的平面角. …………8分
 ∵ 平面ABCD⊥平面ADEF,平面ABCD∩平面ADEF=AD ,ED⊥AD.
∵ 平面ABCD⊥平面ADEF,平面ABCD∩平面ADEF=AD ,ED⊥AD.
∴ ED⊥平面ABCD,
故∠EBD就是直线BE与平面ABCD成的角,…………10分
知∠EBD=45°,设AB=a,则BE=BD= a.
a.
在 ABH中:AH=AB= a,
ABH中:AH=AB= a,
BH= ,AP=
,AP= =
= a.
a.
在 GPA中:由AG=
GPA中:由AG= =
= a
a
=AP ,GA⊥AP,知∠GPA=45°.
故平面GBE与平面ABCD所成的锐二面角的大小为45°.…………12分
19.解:(1)记A0表示事件“取出的2件产品中无二等品”,A1表示事件“取出的2件产品中恰有1件是二等品”.
则A0、A1互斥,且A=A0+A1,
故P (A)=P
(A0+A1)=P
(A0) +P
(A1)=(1-p)2+C p (1-p)=1-p2.
p (1-p)=1-p2.
依题意,知1-p2=0.96,
又p>0,得p=0.2.…………6分
(2)若该批产品共100件,由(1)知,其中共有二等品100×0.2=20件.
记C表示事件“取出的2件产品中无二等品”,
则事件B与事件C互斥,依题意,知
P(C)= .故P (B)=1-P(C)=
.故P (B)=1-P(C)= .…………12分
.…………12分
20.解 (1) 在
在 上单调递增,
上单调递增, 上单调递减,
上单调递减,
 有两根
有两根 ,……3分
,……3分
 ……6分
……6分
(2)令 ,
,
则 ,
……………8分
,
……………8分
因为 在
在 上恒大于0,
上恒大于0,
所以 在
在 上单调递增,
上单调递增,
故 ,
,
 , …………10分
, …………10分
 .
……………12分
.
……………12分
21.解:(1)依题意,知 =10b-b =9b.
=10b-b =9b.
由 0,
0,
得 ,
,
故 =
= ,
,
得 =
= 9b=
9b= b.…………4分
b.…………4分
(2)依题意,知 =
=
由
得
即  -
- =
=
故 =
=
(3)由a、b是互相垂直的单位向量,c = a+b知,b •c= b •( a+b)=0+1=1.
得 an= b •2 n c=2 n
b •2 n c=2 n .记数列{an}的前n项和为Sn,
.记数列{an}的前n项和为Sn,
则有 Sn=2×9+4×3+6×1+8× +…+2 n
+…+2 n .①…………10分
.①…………10分
 Sn=2×3+4×1+6×
Sn=2×3+4×1+6× +8×
+8× +…+2(n-1)
+…+2(n-1) + 2 n
+ 2 n .②
.②
①-②得, Sn=2[9+3+1+
Sn=2[9+3+1+ +…+
+…+ ]- 2 n
]- 2 n .
.
故Sn = .…………12分
.…………12分
22.解:(I)设 依题意得
依题意得

消去 ,整理得
,整理得 .…………4分
.…………4分
当 时,方程表示焦点在
时,方程表示焦点在 轴上的椭圆;
轴上的椭圆;
当 时,方程表示焦点在
时,方程表示焦点在 轴上的椭圆;
轴上的椭圆;
当 时,方程表示圆. …………6分
时,方程表示圆. …………6分
(II)当 时,方程为
时,方程为 ,
,
设直线 的方程为
的方程为 ,
,

消去 得
得 .…………10分
.…………10分
根据已知可得 ,故有
,故有 ,
,
 ,
, 直线
直线 的斜率为
的斜率为 . …………12分
. …………12分
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com