
题目列表(包括答案和解析)
| π |
| 12 |
| 7π |
| 12 |
| 3 |
| 3 |
 ,求函数y=f(x)的解析式,并写出函数f(x)的单调递增区间;
,求函数y=f(x)的解析式,并写出函数f(x)的单调递增区间; 时,在△ABC中,满足
时,在△ABC中,满足 ,且BC=1,若E为BC中点,试求AE的最大值.
,且BC=1,若E为BC中点,试求AE的最大值.已知椭圆![]() 经过点(0,1),离心率
经过点(0,1),离心率![]()
(I)求椭圆C的方程;
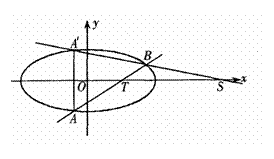 (II)设直线
(II)设直线![]() 与椭圆C交于A,B两点,点A关于x轴的对称点为A’.试问:当m变化时直线
与椭圆C交于A,B两点,点A关于x轴的对称点为A’.试问:当m变化时直线![]() 与x轴是否交于一个定点?若是,请写出定点坐标,并证明你的结论;若不是,请说明理由。
与x轴是否交于一个定点?若是,请写出定点坐标,并证明你的结论;若不是,请说明理由。
已知幂函数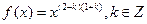 ,且
,且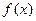 在
在 上单调递增.
上单调递增.
(Ⅰ)求实数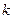 的值,并写出相应的函数
的值,并写出相应的函数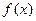 的解析式;
的解析式;
(II)若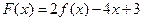 在区间
在区间 上不单调,求实数
上不单调,求实数 的取值范围;
的取值范围;
(III)试判断是否存在正数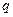 ,使函数
,使函数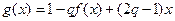 在区间
在区间 上的值域为
上的值域为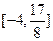 . 若存在,求出
. 若存在,求出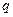 的值;若不存在,请说明理由
的值;若不存在,请说明理由
已知幂函数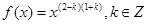 ,且
,且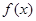 在
在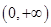 上单调递增.
上单调递增.
(Ⅰ)求实数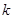 的值,并写出相应的函数
的值,并写出相应的函数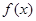 的解析式;
的解析式;
(II)若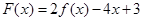 在区间
在区间 上不单调,求实数
上不单调,求实数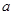 的取值范围;
的取值范围;
(III)试判断是否存在正数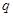 ,使函数
,使函数 在区间
在区间 上的值域为
上的值域为 . 若存在,求出
. 若存在,求出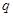 的值;若不存在,请说明理由
的值;若不存在,请说明理由
一、选择题
题号
1
2
3
4
5
6
7
8
9
10
11
12
答案
A
D
C
C
B
B
A
B
C
D
C
D
二、填空题
13.2 14.-1 15.60 16.③④
三、解答题
17.解:(1)∵ ,
, ,
,
∴ .
…………2分
.
…………2分
又 ,
…………4分
,
…………4分
∴ ,∴
,∴ .…………5分
.…………5分
(2)∵ ,
, ,
, ,
,
∴ .
…………7分
.
…………7分
∵ ,
,
∴ . …………9分
. …………9分
 ∴
∴ ,
,
∴ .…………10分
.…………10分
18. (1)证明:连结BD交AC于点M,取BE的中点N,
连结MN,则MN∥ED且MN= ED,依题意,
ED,依题意,
知AG∥ED且AG= ED,
ED,
∴MN∥AG且MN=AG.
故四边形MNAG是平行四边形,
AM∥GN,即AC∥GN,…………4分
又∵ ,
,
∴ AC∥平面GBE. …………6分
(2)延长EG交DA的延长线于H点,
连结BH,作AP⊥BH于P点,连结GP.
∵ 平面ABCD⊥平面ADEF,平面ABCD∩平面ADEF=AD ,
GH 平面ADEF, GA⊥AD.
平面ADEF, GA⊥AD.
∴ GA⊥平面ABCD,由三垂线定理,知GP⊥BH,
故∠GPA就是所求二面角的平面角. …………8分
 ∵ 平面ABCD⊥平面ADEF,平面ABCD∩平面ADEF=AD ,ED⊥AD.
∵ 平面ABCD⊥平面ADEF,平面ABCD∩平面ADEF=AD ,ED⊥AD.
∴ ED⊥平面ABCD,
故∠EBD就是直线BE与平面ABCD成的角,…………10分
知∠EBD=45°,设AB=a,则BE=BD= a.
a.
在 ABH中:AH=AB= a,
ABH中:AH=AB= a,
BH= ,AP=
,AP= =
= a.
a.
在 GPA中:由AG=
GPA中:由AG= =
= a
a
=AP ,GA⊥AP,知∠GPA=45°.
故平面GBE与平面ABCD所成的锐二面角的大小为45°.…………12分
19.解:(1)记A0表示事件“取出的2件产品中无二等品”,A1表示事件“取出的2件产品中恰有1件是二等品”.
则A0、A1互斥,且A=A0+A1,
故P (A)=P
(A0+A1)=P
(A0) +P
(A1)=(1-p)2+C p (1-p)=1-p2.
p (1-p)=1-p2.
依题意,知1-p2=0.96,
又p>0,得p=0.2.…………6分
(2)若该批产品共100件,由(1)知,其中共有二等品100×0.2=20件.
记C表示事件“取出的2件产品中无二等品”,
则事件B与事件C互斥,依题意,知
P(C)= .故P (B)=1-P(C)=
.故P (B)=1-P(C)= .…………12分
.…………12分
20.解 (1) 在
在 上单调递增,
上单调递增, 上单调递减,
上单调递减,
 有两根
有两根 ,……3分
,……3分
 ……6分
……6分
(2)令 ,
,
则 ,
……………8分
,
……………8分
因为 在
在 上恒大于0,
上恒大于0,
所以 在
在 上单调递增,
上单调递增,
故 ,
,
 , …………10分
, …………10分
 .
……………12分
.
……………12分
21.解:(1)依题意,知 =10b-b =9b.
=10b-b =9b.
由 0,
0,
得 ,
,
故 =
= ,
,
得 =
= 9b=
9b= b.…………4分
b.…………4分
(2)依题意,知 =
=
由
得
即  -
- =
=
故 =
=
(3)由a、b是互相垂直的单位向量,c = a+b知,b •c= b •( a+b)=0+1=1.
得 an= b •2 n c=2 n
b •2 n c=2 n .记数列{an}的前n项和为Sn,
.记数列{an}的前n项和为Sn,
则有 Sn=2×9+4×3+6×1+8× +…+2 n
+…+2 n .①…………10分
.①…………10分
 Sn=2×3+4×1+6×
Sn=2×3+4×1+6× +8×
+8× +…+2(n-1)
+…+2(n-1) + 2 n
+ 2 n .②
.②
①-②得, Sn=2[9+3+1+
Sn=2[9+3+1+ +…+
+…+ ]- 2 n
]- 2 n .
.
故Sn = .…………12分
.…………12分
22.解:(I)设 依题意得
依题意得

消去 ,整理得
,整理得 .…………4分
.…………4分
当 时,方程表示焦点在
时,方程表示焦点在 轴上的椭圆;
轴上的椭圆;
当 时,方程表示焦点在
时,方程表示焦点在 轴上的椭圆;
轴上的椭圆;
当 时,方程表示圆. …………6分
时,方程表示圆. …………6分
(II)当 时,方程为
时,方程为 ,
,
设直线 的方程为
的方程为 ,
,

消去 得
得 .…………10分
.…………10分
根据已知可得 ,故有
,故有 ,
,
 ,
, 直线
直线 的斜率为
的斜率为 . …………12分
. …………12分
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com