
题目列表(包括答案和解析)
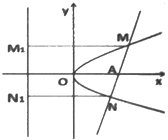 过抛物线y2=2Px(P>0)的对称轴上一点A(a,0)(a>0)的直线与抛物线相交于M,N两点,自M,N向直线l:x=-a作垂线,垂足分别为M1,N1.
过抛物线y2=2Px(P>0)的对称轴上一点A(a,0)(a>0)的直线与抛物线相交于M,N两点,自M,N向直线l:x=-a作垂线,垂足分别为M1,N1.| P | 2 |
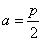 时,求证:AM1⊥AN1;
时,求证:AM1⊥AN1;设点F是抛物线L:y2=2px(p>0)的焦点,P1,P2…,Pn是抛物线L上的n个不同的点n(n≥3,n∈N*)
(1)当p=2时,试写出抛物线L上三点P1、P2、P3的坐标,时期满足|![]() |+|
|+|![]() |+|
|+|![]() |=6;
|=6;
(2)当n≥3时,若![]() +
+![]() +…+
+…+![]() =
=![]() ,求证:|
,求证:|![]() |+|
|+|![]() |+…|
|+…|![]() |=np;
|=np;
(3)当n>3时,某同学对(2)的逆命题,即:“若|![]() |+|
|+|![]() |+…+|
|+…+|![]() |=np,则
|=np,则![]() +
+![]() +…+
+…+![]() =
=![]() ”开展了研究并发现其为假命题.
”开展了研究并发现其为假命题.
请你就此从以下三个研究方向中任选一个开展研究:
①试构造一个说明该命题确实是假命题的反例;
②对任意给定的大于3的正整数n,试构造该假命题反例的一般形式,并说明你的理由;
③如果补充一个条件后能使该命题为真,请写出你认为需要补充的一个条件,并说明加上该条件后,能使该逆命题为真命题的理由
 ;
; ,求证:
,求证: ;
; ,则
,则 ”开展了研究并发现其为假命题.
”开展了研究并发现其为假命题. ;
; ,求证:
,求证: ;
; ,则
,则 ”开展了研究并发现其为假命题.
”开展了研究并发现其为假命题.湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com