
题目列表(包括答案和解析)
(本小题满分12分)
已知直线 经过抛物线
经过抛物线 的焦点,且与抛物线交于
的焦点,且与抛物线交于 两点,点
两点,点 为坐标原点.
为坐标原点.

(Ⅰ)证明: 为钝角.
为钝角.
(Ⅱ)若 的面积为
的面积为 ,求直线
,求直线 的方程;
的方程;
(本小题满分12分)
已知直线 过椭圆
过椭圆 的右焦点
的右焦点 ,抛物线:
,抛物线: 的焦点为椭圆
的焦点为椭圆 的上顶点,且直线
的上顶点,且直线 交椭圆
交椭圆 于
于 、
、 两点,点
两点,点 、
、 、
、 在直线
在直线 上的射影依次为点
上的射影依次为点 、
、 、
、 .
.
(1)求椭圆 的方程;
的方程;
(2)若直线l交y轴于点 ,且
,且 ,当
,当 变化时,探求
变化时,探求 的值是否为定值?若是,求出
的值是否为定值?若是,求出 的值,否则,说明理由;
的值,否则,说明理由;
(3)连接 、
、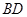 ,试探索当
,试探索当 变化时,直线
变化时,直线 与
与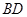 是否相交于定点?若是,请求出定点的坐标,并给予证明;否则,说明理由.
是否相交于定点?若是,请求出定点的坐标,并给予证明;否则,说明理由.
(本小题满分12分)已知直线 过定点
过定点 ,且与抛物线
,且与抛物线 交于
交于 、
、 两点,抛物线在
两点,抛物线在 、
、 两点处的切线的相交于点
两点处的切线的相交于点 .
.
(I)求点 的轨迹方程;
的轨迹方程;
(II)求三角形 面积的最小值.
面积的最小值.

(本小题满分12分)
已知直线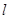 经过抛物线
经过抛物线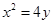 的焦点,且与抛物线交于
的焦点,且与抛物线交于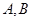 两点,点
两点,点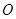 为坐标原点.
为坐标原点.
(Ⅰ)证明: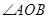 为钝角.
为钝角.
(Ⅱ)若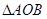 的面积为
的面积为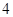 ,求直线
,求直线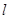 的方程;
的方程;
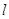 经过抛物线
经过抛物线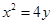 的焦点,且与抛物线交于
的焦点,且与抛物线交于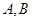 两点,点
两点,点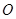 为坐标原点.
为坐标原点.
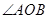 为钝角.
为钝角.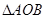 的面积为
的面积为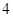 ,求直线
,求直线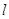 的方程;
的方程;一、选择题:本大题共12小题,每小题5分,共60分.
BCBBA BCDCB DA
二.填空题:本大题共4小题,每小题5分,共20分.
13. 2 14 .
14 .  15.
4 16.
15.
4 16. 
三、解答题(本大题共6小题,共70分,解答应写出文字说明、证明过程或演算步骤)
17. (本大题共10分)
解: 4分
4分
或 8分
8分
故原不等式的解集为 10分
10分
18. (本小题满分12分)
解:(1) ,
, ,且
,且 .
.
 ,即
,即 ,又
,又 ,
, ……..2分
……..2分
又由 ,
, 5分
5分
(2)由正弦定理得: ,
7分
,
7分
又 ,
,
 …………9分
…………9分
 ,则
,则 .则
.则 ,
,
即 的取值范围是
的取值范围是 …………………
12分
…………………
12分
19.(本小题满分12分)
(1)解:设“射手射击1次,击中目标”为事件A
则在3次射击中至少有两次连续击中目标的概率

 =
= 7分
7分
(2)解:射手第3次击中目标时,恰好射击了4次的概率
 12分
12分
20. (本小题满分12分)
(Ⅰ)∵
∴ 2分
2分
∵ 4分
4分
∴ 6分
6分
(Ⅱ)∵函数 在区间
在区间 上单调递增
上单调递增
∴ 对一切
对一切 恒成立
恒成立
方法1  时成立
时成立
当 时,等价于不等式
时,等价于不等式 恒成立
恒成立
令
当 时取到等号,所以
时取到等号,所以
∴ 12分
12分
方法2 设
对称轴
当 时,要满足条件,只要
时,要满足条件,只要 成立
成立
当 时,
时, ,∴
,∴
当 时,只要
时,只要 矛盾
矛盾
综合得 12分
12分
21.(本小题满分12分)
解:(Ⅰ)设 的公差为d,{Bn}的公比为q,则依题意有q>0且
的公差为d,{Bn}的公比为q,则依题意有q>0且

解得d=2,q=2.
所以,  ,
,
 6分
6分
(Ⅱ) 错位相减法得:
错位相减法得: n=1,2,3…
12分
n=1,2,3…
12分
22.(本小题满分12分)
解:(I)由

故 的方程为
的方程为 点A的坐标为(1,0)
2分
点A的坐标为(1,0)
2分
设
由
整理 4分
4分
 M的轨迹C为以原点为中心,焦点在x轴上,长轴长为
M的轨迹C为以原点为中心,焦点在x轴上,长轴长为 ,短轴长为2的椭圆 5分
,短轴长为2的椭圆 5分
(II)如图,由题意知 的斜率存在且不为零,
的斜率存在且不为零,
设 方程为
方程为 ①
①
将①代入 ,整理,得
,整理,得
 7分
7分
设 、
、 ,则
,则 ②
②
令 由此可得
由此可得
由②知

 ,
,
即 10分
10分


解得
又
 面积之比的取值范围是
面积之比的取值范围是 12分
12分
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com