
题目列表(包括答案和解析)
在△ABC中,BA=BC,∠ABC=α,M是AC的中点,P是线段BM上的动点,将线段PA绕点P顺时针旋转2α得到线段PQ.
(1)若α=60°且点P与点M重合(如下图1),线段CQ的延长线交射线BM于点D,请补全图形,并写出∠CDB的度数;
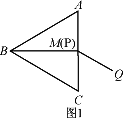
(2)在图2中,点P不与点B,M重合,线段CQ的延长线与射线BM交于点D,猜想∠CDB的大小(用含α的代数式表示),并加以证明;
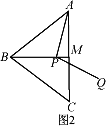
(3)对于适当大小的α,当点P在线段BM上运动到某一位置(不与点B,M重合)时,能使得线段CQ的延长线与射线BM交于点D,且PQ=QD,请直接写出α的范围.
数学探究课上李老师出了这样一道题:“如图,正三角形ABC中有一点P,且PA=3,PB=4,PC=5,试求∠APB的度数.”小明和小军一起讨论时发现了一种求∠APB度数的方法,下面是这种方法的一部分思路.请按照下列思路要求画图或判断.
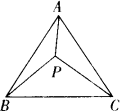
(1)在图中画出△APC绕A点顺时针旋转60°后的图形△AP1B;
(2)试判断△AP1P的形状,并说明理由;
(3)试判断△BP1P的形状,并说明理由;
(4)由2,3两问可知:∠APB=________.
李老师看过后,夸奖了他们,同时提示他们试试以B点或C点为旋转中点,对某个三角形进行适当地旋转,看一看是否可以求出∠APB度数.你认为可以吗?如果可以,给出一种具体的旋转方法;如果不可以,请说明理由.
在课外小组活动时,小伟拿来一道题(原问题)和小熊、小强交流.
原问题:如图1,已知△ABC,∠ACB=90°,∠ABC=45°,分别以AB、BC为边向外作△ABD与△BCE,且DA=DB,EB=EC,∠ADB=∠BEC=90°,连接DE交AB于点F.探究线段DF与EF的数量关系.
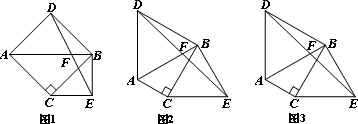
小伟同学的思路是:过点D作DG⊥AB于G,构造全等三角形,通过推理使问
题得解.
小熊同学说:我做过一道类似的题目,不同的是∠ABC=30°,∠ADB=∠BEC=60°.
小强同学经过合情推理,提出一个猜想,我们可以把问题推广到一般情况.
请你参考小慧同学的思路,探究并解决这三位同学提出的问题:
(1)写出原问题中DF与EF的数量关系;
(2)如图2,若∠ABC=30°,∠ADB=∠BEC=60°,原问题中的其他条件不变,你在(1)中得到的结论是否发生变化?请写出你的猜想并加以证明;
(3)如图3,若∠ADB=∠BEC=2∠ABC,原问题中的其他条件不变,你在(1)中得到的结论是否发生变化?请写出你的猜想并加以证明.
某校九年级学习小组在探究学习过程中,用两块完全相同的且含60°角的直角三角板ABC与AFE按如图(1)所示位置放置放置,现将Rt△AEF绕A点按逆时针方向旋转角α(0°<α<90°),如图(2),AE与BC交于点M,AC与EF交于点N,BC与EF交于点P.
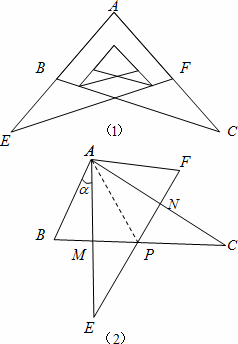
(1)求证:AM=AN;
(2)当旋转角α=30°时,四边形ABPE是什么样的特殊四边形?并说明理由.
阅读下列材料,按要求解答问题:
如图2-1,在ΔABC中,∠A=2∠B,且∠A=60°.小明通过以下计算:由题意,∠B=30°,∠C=90°,c=2b,a=![]() b,得a2-b2=(
b,得a2-b2=(![]() b)2-b2=2b2=b·c.即a2-b2= bc.
b)2-b2=2b2=b·c.即a2-b2= bc.

于是,小明猜测:对于任意的ΔABC,当∠A=2∠B时,关系式a2-b2=bc都成立.
(1)如图2-2,请你用以上小明的方法,对等腰直角三角形进行验证,判断小明的猜测是否正确,并写出验证过程;
(2)如图2-3,你认为小明的猜想是否正确,若认为正确,请你证明;否则,请说明理由;
(3)若一个三角形的三边长恰为三个连续偶数,且∠A=2∠B,请直接写出这个三角形三边的长,不必说明理由.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com