
题目列表(包括答案和解析)
方便、快捷、实惠的电动车是很多人的出行工具。可是,随着电动车的普及,它的安全性也越来越受到人们关注。为了出行更安全,交通部门限制电动车的行驶速度为24km/h。若某款电动车正常行驶遇到紧急情况时,紧急刹车时行驶的路程S(单位:m)和时间t(单位:s)的关系为: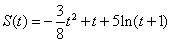 。
。
(Ⅰ)求从开始紧急刹车至电动车完全停止所经过的时间;
(Ⅱ)求该款车正常行驶的速度是否在限行范围内?
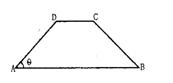
如图,在等腰梯形SBCD中,AB∥CD,且AB=2AD,设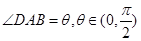 ,以A,B为焦点且过点D的双曲线离心率为
,以A,B为焦点且过点D的双曲线离心率为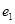 ,以C,D为焦点且过点A的椭圆的离心率为
,以C,D为焦点且过点A的椭圆的离心率为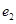 ,则( )
,则( )
 A. 随着
A. 随着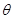 角的增大,
角的增大,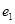 增大,
增大,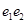 也增大
也增大
B. 随着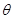 角的增大,
角的增大,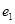 减小,
减小,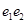 为定值
为定值
C. 随着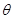 角的增大,
角的增大,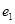 增大,
增大,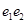 为定值[来源:学+科+网Z+X+X+K]
为定值[来源:学+科+网Z+X+X+K]
D.随着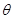 角的增大,
角的增大,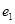 减小,
减小, 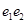 也减小
也减小
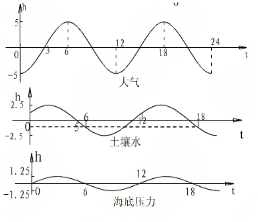 大气、土壤水、海洋等物质在地球表面随着时间的变化而变化,这些物质对地壳压力负荷的变化会引起地壳的变形,在垂直方向尤为明显,根据上海某感测站的观测结果,该地的大气压力负荷、土壤水负荷、以及海底压力负荷引起的地壳垂向位移变化分别依次如图所示.
大气、土壤水、海洋等物质在地球表面随着时间的变化而变化,这些物质对地壳压力负荷的变化会引起地壳的变形,在垂直方向尤为明显,根据上海某感测站的观测结果,该地的大气压力负荷、土壤水负荷、以及海底压力负荷引起的地壳垂向位移变化分别依次如图所示.| π | 6 |
| 2 | 3 |
第I卷(选择题 共60分)
一、选择题(每小题5分,共60分)
1―6ADDCAB 7―12CBBCBC
第Ⅱ卷(非选择题 共90分)
二、填空题(每小题4分,共16分)
13.2 14..files/image172.gif) 15.
15..files/image174.gif) 16.①②
16.①②
三、解答题(本大题共6小题,共74分)
17.解:(I).files/image176.gif)
.files/image178.gif)
.files/image180.gif)
.files/image182.gif) 4分
4分
又.files/image184.gif) 2分
2分
(II).files/image186.gif)
.files/image188.gif) 2分
2分
.files/image190.gif) 1分
1分
.files/image192.gif)
.files/image194.gif)
.files/image196.gif) 3分
3分
18.(I)证明:由题意可知CD、CB、CE两两垂直。
.files/image198.gif) 可建立如图所示的空间直角坐标系
可建立如图所示的空间直角坐标系.files/image200.gif)
则.files/image202.gif) 2分
2分
由.files/image204.gif) 1分
1分
.files/image206.gif)
|