练习册

  • 练习册
  • 试题
    (2)设=.求a+c的值. 【查看更多】

     

    题目列表(包括答案和解析)

    （16分）设，若a,b,c分别为的相应三边长，

    （1）求实数x的取值范围；

    （2）求的最大内角；

    （3）设的外接圆半径为R，内切圆半径为r，求的取值范围。

    查看答案和解析>>

    设函数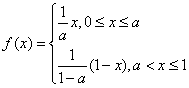        a  为 常数且a∈（0，1）.

    （1）       当a=时，求f（f（））；      

    （2）       若x0满足f（f（x0））= x0,但f（x0）≠x0，则称x0为f（x）的二阶周期点，证明函数有且仅有两个二阶周期点，并求二阶周期点x1，x2；

    （3）       对于（2）中x1，x2，设A（x1,f（f（x1））），B（x2,f（f（x2）））,C(a2,0)，记△ABC的面积为s（a），求s（a）在区间[,]上的最大值和最小值。

    查看答案和解析>>

    在中，角A、B、C的对边分别为

    （1）求角B；

    （2）设的取值范围。

    查看答案和解析>>

    设抛物线C：x2=2py（p＞0）的焦点为F，准线为l，A∈C，已知以F为圆心，FA为半径的圆F交l于B，D两点；
    （1）若∠BFD=90°，△ABD的面积为；求p的值及圆F的方程；
    （2）若A，B，F三点在同一直线m上，直线n与m平行，且n与C只有一个公共点，求坐标原点到m，n距离的比值。

    查看答案和解析>>

    抛物线C的方程为y=ax2（a＜0），过抛物线C上一点P（x0，y0）（x0≠0）作斜率为k1，k2的两条直线分别交抛物线C于A（x1，y1）、B（x2，y2）两点（P、A、B三点互不相同）且满足k2+λk1=0（λ≠0且
    λ≠-1），
    （Ⅰ）求抛物线C的焦点坐标和准线方程；
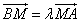    （Ⅱ）设直线AB上一点M，满足，证明线段PM的中点在y轴上；
    （Ⅲ）当λ=1时，若点P的坐标为（1，-1），求∠PAB为钝角时点A的纵坐标y1的取值范围。

    查看答案和解析>>

     

     

    一、选择题

     1―6  DBDCDD   7―12  ADCDCD

    二、填空题

    13．3   14．       15．－25    16．

    三、解答题

    17．（满分12分）

    解：       ∴则       …………3分

      ∴不等式＞a+2     ∵a＜0    ∴＜即＜1+  ……5分

    ①当时，＜0，不等式无解

    ②当时，＜0无解

    ③ 当＜时，＜＜＜＜

    ∴＜x＜＜x                …………10分

    综上所述，原不等式的解集为：

    ①当时，不等式无解

    ②当时，不等式解集为

    ＜x＜或＜x＜                …………12分

    18．（满分12分）

    （1）甲乙两队各五名球员，一个间隔一个排序，出场序的种数是……3分

     

    （2）甲队五名球员，取连续两名的方法数为4。若不考虑乙队，甲队有具只有连续两名队员射中的概率为                      …………………7分

    （3）甲、乙两队点球罚完，再次出现平局，可能的情况以下6种，即均未中球，均中1球，…均中5球，故所求概率为

           …………………12分

    19．（1）∵AA1⊥面ABCD， ∴AA1⊥BD，

    又BD⊥AD， ∴BD⊥A1D                                  …………………2分

    又A1D⊥BE，∴A1D⊥平面BDE                              …………………3分

    （2）连B1C，则B1C⊥BE，易证Rt△CBE∽Rt△CBB1,

    ∴，又E为CC1中点，∴

    ∴                                           ……………………5分

    取CD中点M，连BM，则BM⊥平面CD1，作MN⊥DE于N，连NB，则∠BNM是二面角B―DE―C的平面角            ……………………7分

    Rt△CED中，易求得MN=中，∠BNM=

    ∴∠BNM=arctan                                       …………………10分

    （3）易证BN长就是点B到平面A1DE的距离                    …………………11分

    ∴∠BN=                           …………………12分

    20．（满分12分）

    解：（Ⅰ）由 得。           …………………2分

    由b2=ac及正弦定理得sin2B=sin A sin C.

    于是    cot A + cot C =

    =

    =

    =

    =

    =

    =                              …………………7分

    (Ⅱ)由      ?      =，得，又由，可得，即。

    由余弦定理

                                    …………………9分

    所以                                          …………………12分

    21．（满分13分）

    解：（Ⅰ）              …………………4分

    （Ⅱ）…………………6分

    =                                       …………………8分

                                         …………………9分

    ∴数列是等比数列，且       …………………10分

    （Ⅲ）由（Ⅱ）得：    …………………11分

    ………………12分

                            ………………13分

    22．（满分13分）

    解：（Ⅰ）∵椭圆方程为（a＞b＞0,c＞0,c2=a2－b2）

    ∴,FP的中点D的坐标为（）……2分

    直线AB的方程为：∵D在直线AB上∴……3分

    化简得    ∴…………………4分

    （Ⅱ）…………5分   

           =－3  ∴                                        …………………6分

    由（Ⅰ）得：                                                              …………………7分

    ∴

    ∴椭圆方程为：                                                  …………………8分

    （Ⅲ）设直线QA1和QA2斜率分别为k1、k2，则

    由

    解得……10分由

    解得

    直线MN的方程为令y=0

    得化简得

    ∵∴  ∴

    ∴即直线MN与x轴交于定点（）      ……………13分


    同步练习册答案