
5、y=f(x)与y=f(2a-x){注:y=f(a+x)与y=f(a-x)关于直线x=0对称}关于直线x=a对称。
4、y=f(x)与y=f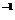 (x)关于直线y=x对称,(或y=f(x)与x=f(y)关于直线y=x对称)。
(x)关于直线y=x对称,(或y=f(x)与x=f(y)关于直线y=x对称)。
3、 y=f(x)与y=-f(-x)关于原点对称。
2、y=f(x)与y=f(-x)关于y轴对称。
1、y=f(x)与y=-f(x)关于x轴对称。
3、反函数的一些性质:(1)反函数的定义域和值域分别是原函数的值域和定义域,称为互调性,(2)定义域上的单调函数必有反函数,且单调性相同(即函数与其反函数在各自的定义域上的单调性相同),对连续函数而言,只有单调函数才有反函数,但非连续的非单调函数也可能有反函数,(3)函数y=f(x)的图象与其反函数y =f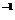 (x)的图象关于直线y=x对称,(4)函数y=f(x)的图象与其反函数y =f
(x)的图象关于直线y=x对称,(4)函数y=f(x)的图象与其反函数y =f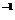 (x)的图象的交点,当它们是递增时,交点在直线y=x上。当它们递减时,交点可以不在直线y=x上,
(x)的图象的交点,当它们是递增时,交点在直线y=x上。当它们递减时,交点可以不在直线y=x上,
如
第四讲:函数图象的对称性与变换
2、求反函数的步骤是:(1)将y=f(x)看成方程,解出x=f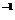 (y)(2)将x,y互换得y =f
(y)(2)将x,y互换得y =f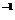 (x)
(x)
(3)写出反函数的定义域,(可根据原函数的定义域或反函数的解析式确定)(4)分段函数的反函数可以分别求出各段函数的反函数再合成。
1、定义:设式子y=f(x)表示y是x的函数,定义域为A,值域为C,从式子y=f(x)中解出x,得到式子x=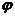 (y),如果对于y在C中的任何一个值,通过式子x=
(y),如果对于y在C中的任何一个值,通过式子x=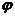 (y),x在A中都有唯一确定的值和它对应,那么式子x=
(y),x在A中都有唯一确定的值和它对应,那么式子x=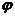 (y)就表示y是x的函数,这样的函数,叫做y=f(x)的反函数,记作x=f
(y)就表示y是x的函数,这样的函数,叫做y=f(x)的反函数,记作x=f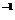 (y),即x=
(y),即x=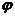 (y)=f
(y)=f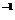 (y),一般对调x=f
(y),一般对调x=f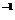 (y)中的字母x,y,把它改写成y =f
(y)中的字母x,y,把它改写成y =f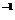 (x)
(x)
5、若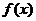 满足
满足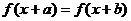 ,那么
,那么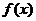 是周期函数,一个周期是
是周期函数,一个周期是
T=|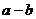 |;
|;
4、定义:对于函数f(x)的定义域内的每个值x都有f(x+T)=f(x)(T¹0),则称f(x)为周期函数,T为它的一个周期。若T为f(x)的周期,则kT也是f(x)的周期,k为任一非0整数。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com