
(2)求离散型随机变量ξ的期望的基本步骤:①理解ξ的意义,写出ξ可能取的全部值;②求ξ取各个值的概率,写出分布列;③根据分布列,由期望的定义求出Eξ  公式E(aξ+b)= aEξ+b,以及服从二项分布的随机变量的期望Eξ=np
公式E(aξ+b)= aEξ+b,以及服从二项分布的随机变量的期望Eξ=np 
3.设有m升水,其中含有大肠杆菌n个.今取水1升进行化验,设其中含有大肠杆菌的个数为ξ,求ξ的数学期望.
分析:任取1升水,此升水中含一个大肠杆菌的概率是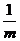 ,事件“ξ=k”发生,即n个大肠杆菌中恰有k个在此升水中,由n次独立重复实验中事件A(在此升水中含一个大肠杆菌)恰好发生k次的概率计算方法可求出P(ξ=k),进而可求Eξ.
,事件“ξ=k”发生,即n个大肠杆菌中恰有k个在此升水中,由n次独立重复实验中事件A(在此升水中含一个大肠杆菌)恰好发生k次的概率计算方法可求出P(ξ=k),进而可求Eξ.
解:记事件A:“在所取的1升水中含一个大肠杆菌”,则P(A)=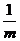 .
.
∴ P(ξ=k)=Pn(k)=C
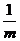 )k(1-
)k(1-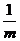 )n-k(k=0,1,2,….,n).
)n-k(k=0,1,2,….,n).
∴ ξ-B(n,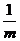 ),故 Eξ =n×
),故 Eξ =n×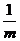 =
=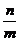

2. 篮球运动员在比赛中每次罚球命中的1分,罚不中得0分.已知某运动员罚球命中的概率为0.7,求
⑴他罚球1次的得分ξ的数学期望;
⑵他罚球2次的得分η的数学期望;
⑶他罚球3次的得分ξ的数学期望.
解:⑴因为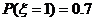 ,
,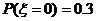 ,所以
,所以
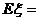 1×
1×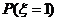 +0×
+0×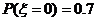
⑵η的概率分布为
|
η |
0 |
1 |
2 |
|
P |
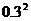 |
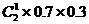 |
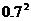 |
所以 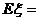 0×
0×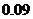 +1×
+1×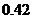 +2×
+2×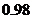 =1.4.
=1.4.
⑶ξ的概率分布为
|
ξ |
0 |
1 |
2 |
3 |
|
P |
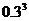 |
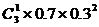 |
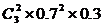 |
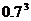 |
所以 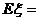 0×
0×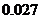 +1×
+1×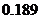 +2×
+2×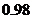 =2.1.
=2.1.
1. 口袋中有5只球,编号为1,2,3,4,5,从中任取3球,以 表示取出球的最大号码,则
表示取出球的最大号码,则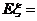 (
)
(
)
A.4; B.5; C.4.5; D.4.75
答案:C 
例1. 篮球运动员在比赛中每次罚球命中得1分,罚不中得0分,已知他命中的概率为0.7,求他罚球一次得分 的期望
的期望
解:因为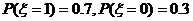 ,
,
所以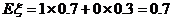

例2. 随机抛掷一枚骰子,求所得骰子点数 的期望
的期望
解:∵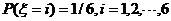 ,
,
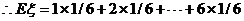 =3.5
=3.5
例3. 有一批数量很大的产品,其次品率是15%,对这批产品进行抽查,每次抽取1件,如果抽出次品,则抽查终止,否则继续抽查,直到抽出次品为止,但抽查次数不超过10次 求抽查次数
求抽查次数 的期望(结果保留三个有效数字)
的期望(结果保留三个有效数字)
解:抽查次数 取1
取1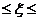 10的整数,从这批数量很大的产品中抽出1件检查的试验可以认为是彼此独立的,取出次品的概率是0.15,取出正品的概率是0.85,前
10的整数,从这批数量很大的产品中抽出1件检查的试验可以认为是彼此独立的,取出次品的概率是0.15,取出正品的概率是0.85,前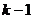 次取出正品而第
次取出正品而第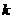 次(
次(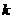 =1,2,…,10)取出次品的概率:
=1,2,…,10)取出次品的概率:
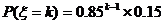 (
(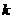 =1,2,…,10)
=1,2,…,10)
需要抽查10次即前9次取出的都是正品的概率: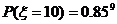
 由此可得
由此可得 的概率分布如下:
的概率分布如下:
 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
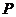 |
0.15 |
0.1275 |
0.1084 |
0.092 |
0.0783 |
0.0666 |
0.0566 |
0.0481 |
0.0409 |
0.2316 |
根据以上的概率分布,可得 的期望
的期望
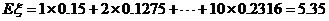

例4. 一次英语单元测验由20个选择题构成,每个选择题有4个选项,其中有且仅有一个选项是正确答案,每题选择正确答案得5分,不作出选择或选错不得分,满分100分  学生甲选对任一题的概率为0.9,学生乙则在测验中对每题都从4个选择中随机地选择一个,求学生甲和乙在这次英语单元测验中的成绩的期望
学生甲选对任一题的概率为0.9,学生乙则在测验中对每题都从4个选择中随机地选择一个,求学生甲和乙在这次英语单元测验中的成绩的期望 
解:设学生甲和乙在这次英语测验中正确答案的选择题个数分别是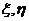 ,则
,则 ~ B(20,0.9),
~ B(20,0.9),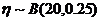 ,
,
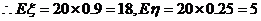

由于答对每题得5分,学生甲和乙在这次英语测验中的成绩分别是5 和5
和5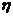
 所以,他们在测验中的成绩的期望分别是:
所以,他们在测验中的成绩的期望分别是:
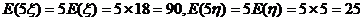

例5.随机的抛掷一个骰子,求所得骰子的点数ξ的数学期望.
解:抛掷骰子所得点数ξ的概率分布为
|
ξ |
1 |
2 |
3 |
4 |
5 |
6 |
|
P |
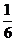 |
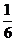 |
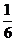 |
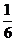 |
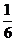 |
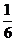 |
所以
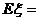 1×
1×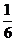 +2×
+2×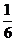 +3×
+3×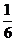 +4×
+4×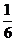 +5×
+5×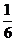 +6×
+6×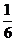
=(1+2+3+4+5+6)×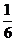 =3.5.
=3.5.
抛掷骰子所得点数ξ的数学期望,就是ξ的所有可能取值的平均值.
例6.某城市出租汽车的起步价为10元,行驶路程不超出4km时租车费为10元,若行驶路程超出4km,则按每超出lkm加收2元计费(超出不足lkm的部分按lkm计).从这个城市的民航机场到某宾馆的路程为15km.某司机经常驾车在机场与此宾馆之间接送旅客,由于行车路线的不同以及途中停车时间要转换成行车路程(这个城市规定,每停车5分钟按lkm路程计费),这个司机一次接送旅客的行车路程ξ是一个随机变量.设他所收租车费为η
(Ⅰ)求租车费η关于行车路程ξ的关系式;
(Ⅱ)若随机变量ξ的分布列为
|
ξ |
15 |
16 |
17 |
18 |
|
P |
0.1 |
0.5 |
0.3 |
0.1 |
求所收租车费η的数学期望.
(Ⅲ)已知某旅客实付租车费38元,而出租汽车实际行驶了15km,问出租车在途中因故停车累计最多几分钟?
解:(Ⅰ)依题意得 η=2(ξ-4)十10,即 η=2ξ+2;
(Ⅱ)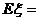
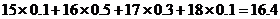
∵ η=2ξ+2
∴ 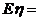 2Eξ+2=34.8 (元)
2Eξ+2=34.8 (元)
故所收租车费η的数学期望为34.8元.
(Ⅲ)由38=2ξ+2,得ξ=18,5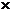 (18-15)=15
(18-15)=15
所以出租车在途中因故停车累计最多15分钟 

5.若ξ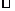 B(n,p),则Eξ=np
B(n,p),则Eξ=np
证明如下:
∵ 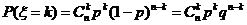 ,
,
∴ 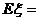 0×
0×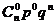 +1×
+1×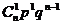 +2×
+2×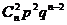 +…+k×
+…+k×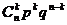 +…+n×
+…+n×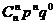 .
.
又∵ 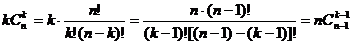 ,
,
∴ 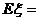
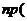
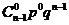 +
+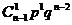 +…+
+…+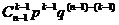 +…+
+…+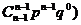
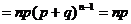 .
.
故 若ξ-B(n,p),则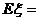 np.
np.
4. 期望的一个性质:若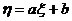 (a、b是常数),ξ是随机变量,则η也是随机变量,它们的分布列为
(a、b是常数),ξ是随机变量,则η也是随机变量,它们的分布列为
|
ξ |
x1 |
x2 |
… |
xn |
… |
|
η |
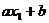 |
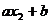 |
… |
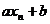 |
… |
|
P |
p1 |
p2 |
… |
pn |
… |
于是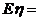
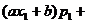
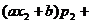 …
…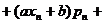 …
…
=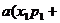
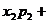 …
…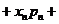 …)
…)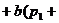
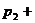 …
…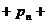 …)
…)
=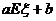 ,
,
由此,我们得到了期望的一个性质: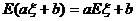
3. 平均数、均值:一般地,在有限取值离散型随机变量ξ的概率分布中,令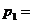
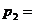 …
…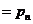 ,则有
,则有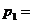
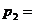 …
…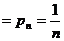 ,
,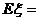
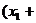
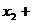 …
…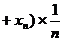 ,所以ξ的数学期望又称为平均数、均值
,所以ξ的数学期望又称为平均数、均值

2. 数学期望是离散型随机变量的一个特征数,它反映了离散型随机变量取值的平均水平 
根据已知随机变量的分布列,我们可以方便的得出随机变量的某些制定的概率,但分布列的用途远不止于此,例如:已知某射手射击所得环数ξ的分布列如下
|
ξ |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
|
P |
0.02 |
0.04 |
0.06 |
0.09 |
0.28 |
0.29 |
0.22 |
在n次射击之前,可以根据这个分布列估计n次射击的平均环数.这就是我们今天要学习的离散型随机变量的期望

根据射手射击所得环数ξ的分布列,
我们可以估计,在n次射击中,预计大约有
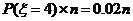 次得4环;
次得4环;
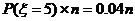 次得5环;
次得5环;
…………
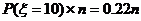 次得10环.
次得10环.
故在n次射击的总环数大约为
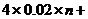
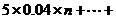
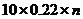
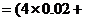
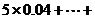
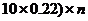 ,
,
从而,预计n次射击的平均环数约为
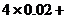
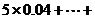
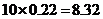 .
.
这是一个由射手射击所得环数的分布列得到的,只与射击环数的可能取值及其相应的概率有关的常数,它反映了射手射击的平均水平.
对于任一射手,若已知其射击所得环数ξ的分布列,即已知各个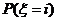 (i=0,1,2,…,10),我们可以同样预计他任意n次射击的平均环数:
(i=0,1,2,…,10),我们可以同样预计他任意n次射击的平均环数:
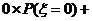
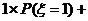 …
…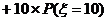 .
.
1.数学期望: 一般地,若离散型随机变量ξ的概率分布为
|
ξ |
x1 |
x2 |
… |
xn |
… |
|
P |
p1 |
p2 |
… |
pn |
… |
则称 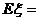
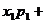
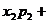 …
…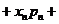 … 为ξ的数学期望,简称期望.
… 为ξ的数学期望,简称期望.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com