
2. 已知全集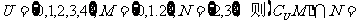
A. 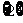 B.
B.
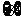 C.
C.
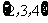 D.
D.
1.已知集合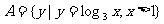 ,
,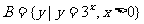 ,则
,则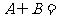
A 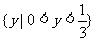 B
B 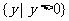 C
C 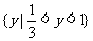 D
D 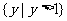
2.三角函数的最值都是在给定区间上取得的,因而特别要注意题设中所给出的区间.
(1)求三角函数最值时,一般要进行一些代数变换和三角变换,要注意函数有意义的条件及弦函数的有界性.
(2)含参数函数的最值问题,要注意参数的作用和影响.
对于含有sinx±cosx,sinxcosx的函数的最值问题,常用的方法是令sinx±cosx=t,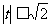 ,将sinxcosx转化为t的函数关系式,从而化为二次函数的最值问题。
,将sinxcosx转化为t的函数关系式,从而化为二次函数的最值问题。
例14.求y=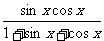 的最值?
的最值?
思悟小结
1.求三角函数最值的常用方法有:①配方法(主要利用二次函数理论及三角函数的有界性);②化为一个角的三角函数(主要利用和差角公式及三角函数的有界性);③数形结合法(常用到直线的斜率关系);④换元法(如万能公式,将三角问题转化为代数问题);⑤基本不等式法等.
例13.求函数y=x+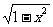 的最大、最小值
的最大、最小值
解:∵x R
∴可设x=sin
R
∴可设x=sin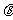 (-
(-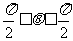 )
)
则有y=sin  +∣cos
+∣cos 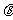 ∣
∣
∵-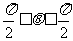 ∴cos
∴cos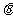 ≥0
≥0
∴y=sin 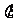 + cos
+ cos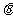 =
=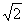 sin(
sin(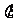 +
+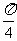 )
)
∵-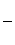
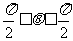 ∴-
∴-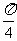 ≤
≤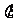 ≤+
≤+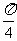 ≤
≤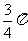
∴-1≤sin(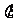 +
+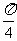 )
)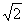
当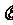 =-
=-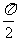 亦即x=-1 函数y
亦即x=-1 函数y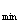 =-1
=-1
当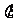 =
=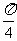 亦即x=
亦即x=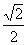 函数y
函数y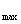 =
=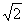
上述例中都运用了三角代换能使某些代数函数的最值问题得到最解决。在这类题型的解题中,必需确定所设三角中角的变化范围,这是十分重要的环节,否则在后面的解题就得分类讨论或者发生矛盾的现象,甚至使整题前功尽弃。
例10.求函数y = 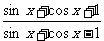 的最小值 (0< x <
的最小值 (0< x < 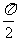 )
)
解:∴0 < x < 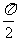 ∵sin x + cos x – 1 ≠0
∵sin x + cos x – 1 ≠0
y = 1 + 
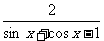 = 1+
= 1+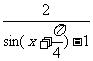 (0 < x <
(0 < x < 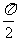 )
)
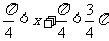 ∴0 <
∴0 < 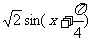 -1 ≤
-1 ≤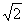 -1
-1
∴y≥1+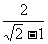 =3+2
=3+2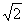
∴函数y在0 < x 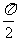 范围内的最小值3+2
范围内的最小值3+2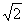
这是一例分子、分母只有常数项不同的三角函数式,便可以在分子中添置辅助项后,通过恒等变形把它化成只有分母含有自变量的三角函数式,只需研究分母的最值,就能求出原函数的最值。在这样的变形中若遇到要把分子“翻下去”作为繁分式分母一部分时,这个“翻下去”的式子不能为零,如果这个式子可能为零,则应将为零的情况另作处理。“设其不为零的”情况下继续解下去,最后把各种情况下求得的值综合起来考虑最值。
例11..y=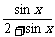 的最大值是_________,最小值是_________.
的最大值是_________,最小值是_________.
解析一:y=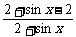 =1-
=1-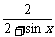 .
.
当sinx=-1时,得ymin=-1,
当sinx=1时,得ymax=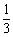 .
.
解析二:原式 sinx=
sinx=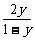 (∵y≠1)
(∵y≠1)
 |
|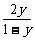 |≤1
|≤1 -1≤y≤
-1≤y≤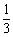 .
.
∴ymax=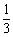 ,ymin=-1.
,ymin=-1.
答案: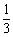 -1
-1
例12..y=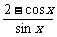 (0<x<π)的最小值是________.
(0<x<π)的最小值是________.
解析一:y=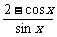
 ysinx+cosx=2
ysinx+cosx=2
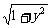 sin(x+
sin(x+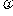 )=2
)=2
 sin(x+
sin(x+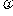 )=
)=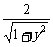 (x∈(0,π))
(x∈(0,π))
 0<
0<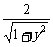 ≤1
≤1 y≥
y≥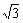 .
.
∴ymin=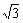 .
.
解析二:y可视为点A(-sinx,cosx),B(0,2)连线的斜率kAB,而点A的轨迹
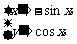 x∈(0,π)是单位圆在第二、三象限的部分(如下图),易知当A(-
x∈(0,π)是单位圆在第二、三象限的部分(如下图),易知当A(-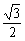 ,
,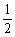 )时,ymin=kAB=
)时,ymin=kAB=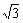 .
.
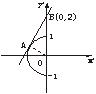
例6.已知:定义在 上的减函数
上的减函数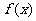 ,使得
,使得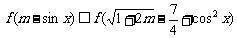
对一切实数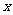 均成立,求实数
均成立,求实数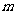 的范围。
的范围。
解:由题意可得 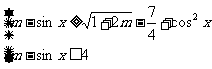 ,
,
即 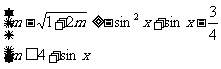
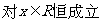 ,
,
又
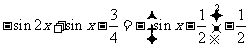 ,
, 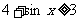 ,
,
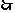
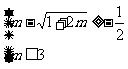 ,
, 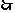
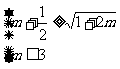 ,
,
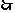
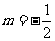 , 或
, 或  .
.
例7.如果∣x∣≤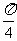 求函数f(x)=cos2x + sin x 的最大、最小值。
求函数f(x)=cos2x + sin x 的最大、最小值。
解:y= -- sin2x + sin x + 1 = --(sin x --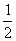 )2 +
)2 + 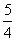
设
sin x = t 得y = --(t -- 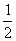 )2 +
)2 + 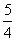 由题设∣x∣≤
由题设∣x∣≤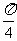 .
.
∴ -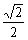 ≤sin x ≤
≤sin x ≤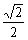 ∴-
∴- 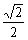 ≤ t ≤
≤ t ≤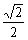
因为f(x)在[-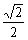 ,
,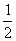 ]是增函数,在[
]是增函数,在[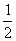 ,
,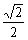 ]是减函数
]是减函数
∴当x = -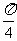 时,
时,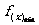 =
= 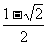
当x = 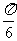 时,
时, 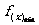 =
= 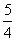
上例就是利用在闭区间上求二次函数最值的方法,就可以求含三角式的二次函数的最值。但是在运用这个方法前,首先要将引用三角比之间的转换使式子中只含有同名的三角比,再把此三角比视为二次函数的自变量。
例8、在△ABC中,求cosAcosBcosC的最大值。
本题是一个经典习题,有多种解法。下面解法中把角C当作主元化为二次形式,再进行配方,又利用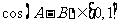 ,此法具有一般性。
,此法具有一般性。

例9.设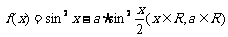 。求f (x)的最大、小值。
。求f (x)的最大、小值。
分析:二次函数,分类讨论
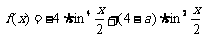 。令
。令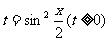 。所以
。所以
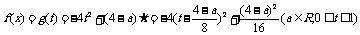
则ⅰ)当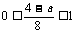 时,即:-4≤a≤4时,
时,即:-4≤a≤4时,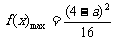 ;当 -4≤a≤0时,
;当 -4≤a≤0时,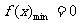 ;当 0≤a≤4时,
;当 0≤a≤4时,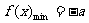 ;
;
ⅱ)当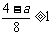 时,即a≤-4,
时,即a≤-4,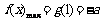 ;
;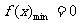 。
。
ⅲ)当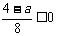 时,即a≥4,
时,即a≥4,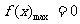 ;
;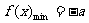 。
。
处理方法:引入辅助角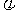 ,化为y=
,化为y=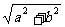 sin(x+
sin(x+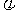 ),利用函数
),利用函数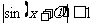 即可求解。Y=asin
即可求解。Y=asin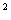 x+bsinxcosx+mcos
x+bsinxcosx+mcos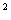 x+n型亦可以化为此类。
x+n型亦可以化为此类。
例3 。已知f(x)=2cos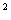 x+
x+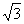 sin2x+a,若x
sin2x+a,若x <2,求a的取值范围。
<2,求a的取值范围。

注:本题综合运用三角恒等变形,三角函数的单调性,不等式的性质,函数的恒成立等知识,是一个较好的三角函数综合题。
例4.求函数y=a sin x + b cos x的最值。
解:y=a sin x + b cos x= sin(x + arc tg
sin(x + arc tg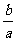 )
)
∴当x=2k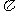 +
+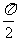 --arc tg
--arc tg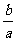 时,ymax =
时,ymax =
当x=2k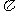 +
+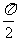 --arc tg
--arc tg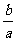 时,ymin =--
时,ymin =--
例5.求函数y= sin2x+2sinx cosx+3 cos2x的最小值、最大值。并写出函数y 取
最值时的x的集合。
解:∵y= sin 2x + 2cos2x
+ 1 = sin 2x + cos 2x + 2 = 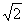 sin(2x +
sin(2x +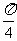 )+ 2
)+ 2
∴当sin(2x +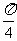 )= --1时, 有ymin = 2 --
)= --1时, 有ymin = 2 --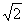 .
.
当sin(2x +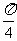 )= 1时,有ymax =
2 +
)= 1时,有ymax =
2 +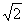 .
.
此时有2x +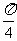 = 2k
= 2k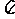 --
--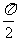 , x = k
, x = k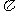 --
--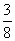
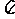 (k
(k z)
z)
2x +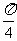 = 2k
= 2k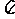 +
+ 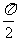 , x = k
, x = k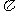 +
+ 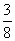 (k
(k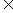 z)
z)
故函数y取最小值2--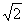 时x 的集合是{x∣x = k
时x 的集合是{x∣x = k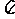 --
--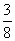
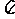 , k
, k z }
z }
y取最大值2 +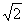 时x 的集合是{x∣x = k
时x 的集合是{x∣x = k +
+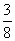
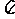 , k
, k z }
z }
从上面三例可以清晰地看出,这一类的三角函数的最值求解中运用的基本的方法是“利用辅助角法”,将较复杂的三角式转化成“Asin(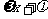 )” 的形式,将异名三角比化归成同名三角比。同时,也应对自变量的取值范围要仔细地考察。
)” 的形式,将异名三角比化归成同名三角比。同时,也应对自变量的取值范围要仔细地考察。
处理方法:利用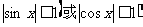 ,即可求解,此时必须注意字母a的符号对最值的影响。
,即可求解,此时必须注意字母a的符号对最值的影响。
例1 函数y=acosx+b(a、b为常数),若-7≤y≤1,求bsinx+acosx的最大值.
剖析:函数y=acosx+b的最值与a的符号有关,故需对a分类讨论.
解:当a>0时,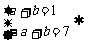 a=4,b=-3;
a=4,b=-3;
当a=0时,不合题意;
当a<0时,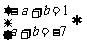 a=-4,b=-3.
a=-4,b=-3.
当a=4,b=-3时,bsinx+acosx=-3sinx+4cosx=5sin(x+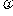 )(tan
)(tan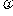 =-
=-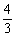 );
);
当a=-4,b=-3时,bsinx+acosx=-3sinx-4cosx=5sin(x+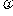 )(tan
)(tan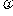 =
=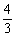 ).
).
∴bsinx+acosx的最大值为5.
例2.例3 已知函数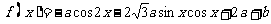 的定义域为
的定义域为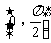 ,值域为
,值域为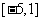 ,求常数
,求常数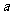 、
、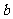 的值.
的值.
解:∵
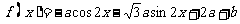 ,
,
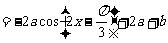 .
.
∵ 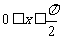 ,∴
,∴ 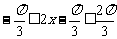 ,∴
,∴ 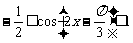 .
.
当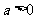 时,
时,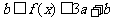 .
.
∴ 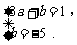 解得
解得 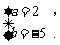
当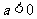 时,
时,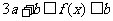 .
.
∴ 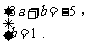 解得
解得 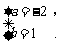
故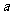 、
、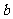 的值为
的值为 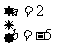 或
或 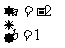
感悟:分类讨论是重要的数学思想方法,本例若不对常数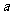 进行讨论,将会出错。
进行讨论,将会出错。
20.(14分)已知函数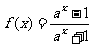 (a>1).
(a>1).
(1)判断函数f (x)的奇偶性;
(2)求f (x)的值域;
(3)证明f (x)在(-∞,+∞)上是增函数.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com