
66. [2010•江西理数]点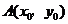 在双曲线
在双曲线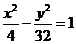 的右支上,若点A到右焦点的距离等于
的右支上,若点A到右焦点的距离等于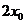 ,则
,则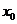 =
=
[答案] 2
[解析]考查圆锥曲线的基本概念和第二定义的转化,读取a=2.c=6,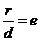
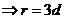 ,
,
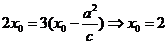
65. [2010•全国卷2文数]已知抛物线C:y2=2px(p>0)的准线l,过M(1,0)且斜率为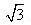 的直线与l相交于A,与C的一个交点为B,若
的直线与l相交于A,与C的一个交点为B,若 ,则p=_________
,则p=_________
[答案]2
[解析]设直线AB: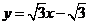 ,代入
,代入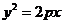 得
得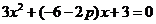 ,又∵
,又∵
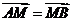 ,∴
,∴
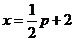 ,解得
,解得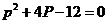 ,解得
,解得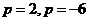 (舍去)。
(舍去)。
64. [2010•全国卷2理数]已知抛物线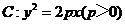 的准线为,过
的准线为,过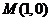 且斜率为
且斜率为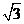 的直线与相交于点
的直线与相交于点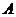 ,与
,与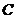 的一个交点为
的一个交点为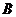 .若
.若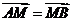 ,则
,则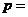 .
.
[答案]2
[解析]过B作BE垂直于准线于E,∵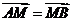 ,∴M为中点,∴
,∴M为中点,∴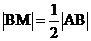 ,又斜率为
,又斜率为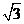 ,
,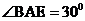 ,∴
,∴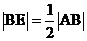 ,∴
,∴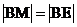 ,∴M为抛物线的焦点,
,∴M为抛物线的焦点,
∴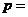 2.
2.
63. [2010•浙江理数]设抛物线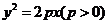 的焦点为
的焦点为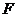 ,点
,点
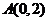 .若线段
.若线段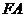 的中点
的中点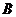 在抛物线上,则
在抛物线上,则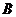 到该抛物线准线的距离为_____________。
到该抛物线准线的距离为_____________。
[答案]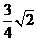
[解析]利用抛物线的定义结合题设条件可得出p的值为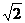 ,B点坐标为(
,B点坐标为(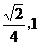 )所以点B到抛物线准线的距离为
)所以点B到抛物线准线的距离为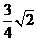 ,本题主要考察抛物线的定义及几何性质,属容易题
,本题主要考察抛物线的定义及几何性质,属容易题
62. [2010•上海文数]动点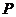 到点
到点 的距离与它到直线
的距离与它到直线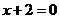 的距离相等,则
的距离相等,则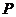 的轨迹方程为 。
的轨迹方程为 。
[答案]y2=8x
[解析]考查抛物线定义及标准方程定义知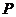 的轨迹是以
的轨迹是以 为焦点的抛物线,p=2所以其方程为y2=8x
为焦点的抛物线,p=2所以其方程为y2=8x
61.[2010 ·四川省绵阳南山中学四月模拟]双曲线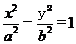 (a>0,b>0)的一个焦点为F1,顶点为A1、A2,P是双曲线上任意一点,则分别以线段PF1,A1A2为直径的两圆一定
(a>0,b>0)的一个焦点为F1,顶点为A1、A2,P是双曲线上任意一点,则分别以线段PF1,A1A2为直径的两圆一定

 ( )
( )
A.相交 B.相切
C.相离 D.以上情况都有可能
[答案]B
[解析]不失一般性设点P为双曲线右支上一点,连PF1,PF2,设PF1的中点为M,设M为以PF1为直径的圆的圆心,连MO,则|MO|=|PF2|==|PF1|-a,即两圆的圆心距等于两圆的半径之差,所以两圆相内切,当点P位于左支上时,同理可证两圆相外切。故选B。
60.[2010·河南省郑州市第二次质检]已知点F是双曲线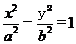 (a>0,b>0)的左焦点,点E是该双曲线的右顶点,过点F且垂直于x轴的直线与双曲线交于A、B两点,△ABE是锐角三角形,则该双曲线的离心率e的取值范围是( )
(a>0,b>0)的左焦点,点E是该双曲线的右顶点,过点F且垂直于x轴的直线与双曲线交于A、B两点,△ABE是锐角三角形,则该双曲线的离心率e的取值范围是( )
A.(1,+∞) B.(1,2) C.(1,1+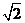 ) D.(2,1+
) D.(2,1+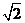 )
)
[答案]B
[解析]由AB⊥x轴,所以△ABE为等腰三角形,又△ABE是锐角三角形,所以∠AEB为锐角,即∠AEF<45º,于是|AF|<|EF|,<a+c,于是c2-a2<a2+ac,即e2-e-2<0,解得-1<e<2,又双曲线的离心率e>1,从而1<e<2。
59.[2010·广西南宁市第二次适应性测试]设F为抛物线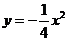 的焦点,与抛物线相切于点P(-4,-4)的直线
的焦点,与抛物线相切于点P(-4,-4)的直线 与x轴的交点为Q,则
与x轴的交点为Q,则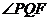 等于( )
等于( )
A. 30° B. 45° C. 60° D. 90°
[答案]D
[解析]易知F(0,-1),又y'=-x,所以kPQ=2,所以直线l的方程为y+4=2(x+4),令y=0,得Q(-2,0),所以kQF==-,所以PQ⊥QF,即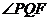 =90º。
=90º。
58.[2010·福州三中五月模拟]若点P是以F1,F2为焦点的椭圆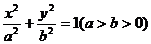 上一点,且
上一点,且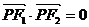 ,
,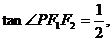 则此椭圆的离心率e=( )
则此椭圆的离心率e=( )
A.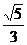 B.
B.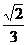 C.
C.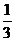 D.
D.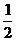
[答案]A
[解析]因为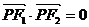 ,即PF1⊥PF2,所以|PF1|2+|PF2|2=4c2,又因为
,即PF1⊥PF2,所以|PF1|2+|PF2|2=4c2,又因为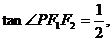 所以|PF1|=2|PF2|。由椭圆的定义知:|PF1|+|PF2|=2a,即3|PF2|=2a,即|PF2|=a,代入|PF1|2+|PF2|2=4c2,解得e==
所以|PF1|=2|PF2|。由椭圆的定义知:|PF1|+|PF2|=2a,即3|PF2|=2a,即|PF2|=a,代入|PF1|2+|PF2|2=4c2,解得e==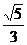 .
.
57.[2010·甘肃省兰州市五月实战模拟]已知定点A(1,0)和定直线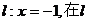 上有两动点E,F且满足
上有两动点E,F且满足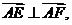 另有动点P,满足
另有动点P,满足 (O为坐标原点),且动点P的轨迹方程为(
)
(O为坐标原点),且动点P的轨迹方程为(
)
A.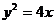 B.
B.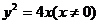 C.
C.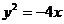 D.
D.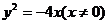
[答案]B
[解析]设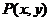 ,
,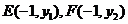 (
(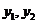 均不为零)由
均不为零)由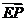 ∥
∥
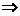
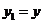 ,即
,即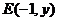 .由
.由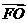 ∥
∥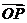
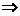
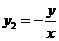 .由
.由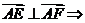
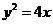
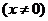 .故选B.
.故选B.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com