
16.(每小题满分12分)
已知向量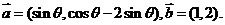
(Ⅰ)若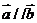 ,求
,求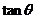 的值;
的值; 

(Ⅱ)若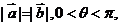 求
求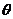 的值。
的值。
解:(Ⅰ) 因为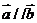 ,所以
,所以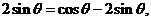
于是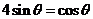 ,故
,故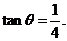
(Ⅱ)由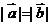 知,
知,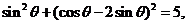
所以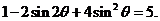
从而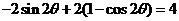 ,即
,即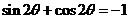 ,
,
于是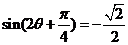 .又由
.又由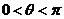 知,
知,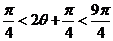 ,
,
所以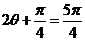 ,或
,或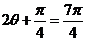 .
.
因此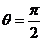 ,或
,或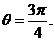
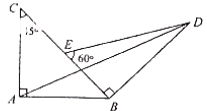
15.如图2,两块斜边长相等的直角三角板拼在一起,若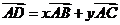 ,则
,则
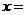
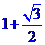 ,
,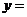
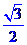 .
.
图2
解:作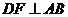 ,设
,设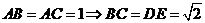 ,
,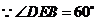 ,
,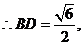
由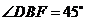 解得
解得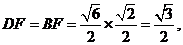 故
故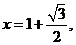
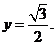
14.在锐角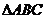 中,
中,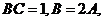 则
则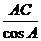 的值等于 2 ,
的值等于 2 ,
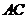 的取值范围为
的取值范围为
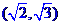 .
. 

解: 设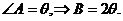 由正弦定理得
由正弦定理得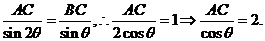
由锐角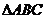 得
得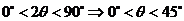 ,
,
又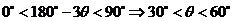 ,故
,故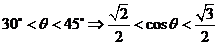 ,
,
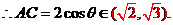
13.过双曲线C: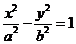
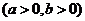 的一个焦点作圆
的一个焦点作圆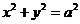 的两条切线,
的两条切线,
切点分别为A,B,若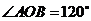 (O是坐标原点),则双曲线线C的离心率为
2
.
(O是坐标原点),则双曲线线C的离心率为
2
.
解: 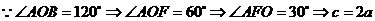 ,
, 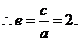
12. 一个总体分为A,B两层,用分层抽样方法从总体中抽取一个容量为10的样本。
已知B层中每个个体被抽到的概率都为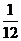 ,则总体中的个体数为 120 .
,则总体中的个体数为 120 .
解: 设总体中的个体数为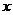 ,则
,则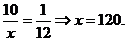
11.在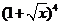 的展开式中,
的展开式中,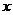 的系数为
6 (用数字作答).
的系数为
6 (用数字作答).
解: 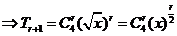 ,故
,故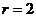 得
得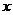 的系数为
的系数为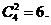
10.若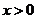 ,则
,则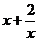 的最小值为
的最小值为 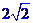 .
. 

解: 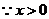
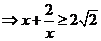 ,当且仅当
,当且仅当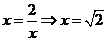 时取等号.
时取等号.
把答案填在答题卡中对应题号后的横线上。
9.某班共30人,其中15人喜爱篮球运动,10人喜爱乒乓球运动,8人对这两项
运动都不喜爱,则喜爱篮球运动但不喜爱乒乓球运动的人数为 12 .
解: 设所求人数为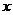 ,则只喜爱乒乓球运动的人数为
,则只喜爱乒乓球运动的人数为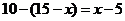 ,
,
故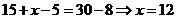 . 注:最好作出韦恩图!
. 注:最好作出韦恩图!
8.设函数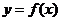 在
在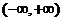 内有定义,对于给定的正数K,定义函数
内有定义,对于给定的正数K,定义函数
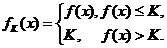
取函数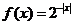 。当
。当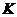 =
=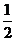 时,函数
时,函数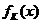 的单调递增区间为[ C ]
的单调递增区间为[ C ]
A .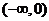 B.
B.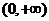 C .
C .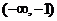 D .
D .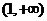
解: 函数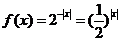 ,作图易知
,作图易知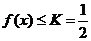
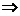
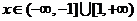 ,
,
故在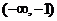 上是单调递增的,选C.
上是单调递增的,选C.


7.若函数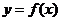 的导函数在区间
的导函数在区间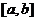 上是增函数,
上是增函数,
则函数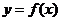
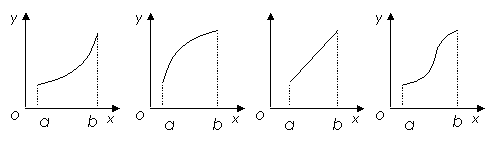 在区间
在区间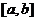 上的图象可能是[ A ]
上的图象可能是[ A ]
|
A . B. C. D.
解: 因为函数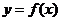 的导函数
的导函数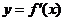 在区间
在区间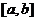 上是增函数,即在区间
上是增函数,即在区间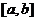 上
上
各点处的斜率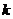 是递增的,由图易知选A. 注意C中
是递增的,由图易知选A. 注意C中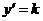 为常数噢.
为常数噢.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com