
天体运动的本来模式与近似模式的差距,近似处理的依据。
3、万有引力做功也具有只与初末位置有关而与路径无关的特征。因而相互作用的物体间有引力势能。在任一惯性系中,若规定相距无穷远时系统的万有引力势能为零,可以证明,当两物体相距为r时系统的万有引力势能为EP
= -G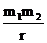

2、条件
a、基本条件
b、拓展条件:
球体(密度呈球对称分布)外部空间的拓展----对球体外一点A的吸引等效于位于球心的质量为球的质量的质点对质点A的吸引;
球体(密度呈球对称分布)内部空间的拓展“剥皮法则”-----对球内任一距球心为r的一质点A的吸引力等效于质量与半径为 r的球的质量相等且位于球心的质点对质点A的吸引;
球壳(密度呈球对称分布)外部空间的拓展----对球壳外一点A的吸引等效于位于球心的质量为球壳的质量的质点对质点A的吸引;
球体(密度呈球对称分布)内部空间的拓展-----对球壳内任一位置上任一质点A的吸引力都为零;
并且根据以为所述,由牛顿第三定律,也可求得一质点对球或对球壳的吸引力。
c、不规则物体间的万有引力计算--分割与矢量叠加
1、定律内容
2、圆周运动
匀速圆周运动的处理:运动学参量v、ω、n、a、f、T之间的关系,向心力的寻求于合成;临界问题的理解。
变速圆周运动:使用自然坐标分析法,一般只考查法向方程。
1、抛体运动(类抛体运动)
关于抛体运动的分析,和新课教材“平跑运动”的分析基本相同。在坐标的选择方面,有灵活处理的余地。
2、两种分解的思路
a、固定坐标分解(适用于匀变速曲线运动)
建立坐标的一般模式--沿加速度方向和垂直加速度方向建直角坐标;提高思想--根据解题需要建直角坐标或非直角坐标。
b、自然坐标分解(适用于变加速曲线运动)
基本常识:在考查点沿轨迹建立切向τ、法向n坐标,所有运动学矢量均沿这两个方向分解。
动力学方程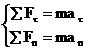 ,其中
,其中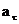 改变速度的大小(速率),
改变速度的大小(速率),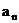 改变速度的方向。且
改变速度的方向。且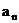 = m
= m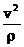 ,其中ρ表示轨迹在考查点的曲率半径。定量解题一般只涉及法向动力学方程。
,其中ρ表示轨迹在考查点的曲率半径。定量解题一般只涉及法向动力学方程。
1、法则与对象
2、参量特征
1、概念、性质
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com