
17.(14分)函数f(x)对一切实数x,y均有f(x+y)-f(y)=(x+2y+1)x成立,且f(1)=0.
(1)求f(0);
(2)求f(x);
(3)不等式f(x)>ax-5当0<x<2时恒成立,求a的取值范围.
解 (1)令x=1,y=0,
得f(1+0)-f(0)=(1+2×0+1)·1=2,
∴f(0)=f(1)-2=-2.
(2)令y=0,f(x+0)-f(0)=(x+2×0+1)·x=x2+x,
∴f(x)=x2+x-2.
(3)f(x)>ax-5化为x2+x-2>ax-5,
ax<x2+x+3,∵x∈(0,2),
∴a<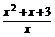 =1+x+
=1+x+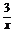 .
.
当x∈(0,2)时,1+x+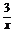 ≥1+2
≥1+2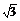 ,当且仅当x=
,当且仅当x=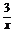 ,即x=
,即x=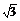 时取等号,由
时取等号,由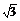 ∈(0,2),得
∈(0,2),得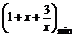 =1+2
=1+2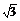 .
.
∴a<1+2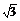 .
.
16.(2008·苏南四市模拟)(14分)甲、乙两公司同时开发同一种新产品,经测算,对于函数f(x),g(x)以及任意的x≥0,当甲公司投入x万元做宣传时,若乙公司投入的宣传费小于f(x)万元,则乙公司对这一新产品的开发有失败的风险,否则没有失败的风险;当乙公司投入x万元做宣传时,若甲公司投入的宣传费小于g(x)万元,则甲公司这一新产品的开发有失败的风险,否则没有失败的风险.
(1)试解释f(0)=10,g(0)=20的实际意义;
(2)设f(x)= 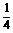 x+10,g(x)=
x+10,g(x)=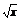 +20,甲、乙两公司为了避免恶性竞争,经过协商,同意在双方均无失败风险的情况下尽可能少地投入宣传费用,问甲、乙两公司各应投入多少宣传费?
+20,甲、乙两公司为了避免恶性竞争,经过协商,同意在双方均无失败风险的情况下尽可能少地投入宣传费用,问甲、乙两公司各应投入多少宣传费?
解 (1)f(0)=10表示当甲公司不投入宣传费时,乙公司要避免新产品的开发有失败的风险,至少要投入10万元宣传费;g(0)=20表示当乙公司不投入宣传费时,甲公司要避免新产品的开发有失败的风险,至少要投入20万元宣传费.
(2)设甲公司投入宣传费x万元,乙公司投入宣传费y万元,依题意,当且仅当
|
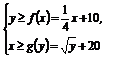 时,
时,
双方均无失败的风险.
由①②得y≥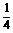 (
(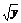 +20)+10,即4y-
+20)+10,即4y-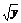 -60≥0,
-60≥0,
即(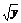 -4)(4
-4)(4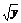 +15)≥0.
+15)≥0.
∵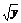 ≥0,∴4
≥0,∴4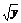 +15>0.
+15>0.
∴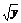 ≥4.∴y≥16.∴x≥
≥4.∴y≥16.∴x≥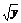 +20≥4+20=24.
+20≥4+20=24.
∴xmin=24,ymin=16,
即在双方均无失败风险的情况下,甲公司至少要投入24万元,乙公司至少要投入16万元.
15.(2008·石家庄模拟)(14分)已知a=(1,x),b=(x2+x,-x),m为常数且m≤-2,求使不等式a·b+2>m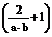 成立
成立
的x的范围.
解 ∵a=(1,x),b=(x2+x,-x),
∴a·b=x2+x-x2=x.
由a·b+2>m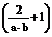
?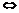 x+2>m
x+2>m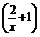
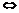 (x+2)-m
(x+2)-m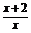 >0
>0
?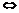 x(x+2)(x-m)>0(m≤-2).
x(x+2)(x-m)>0(m≤-2).
①当m=-2时,原不等式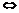 x(x+2)2>0
x(x+2)2>0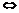 x>0;
x>0;
②当m<-2时,原不等式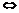 m<x<-2或x>0.
m<x<-2或x>0.
综上,得m=-2时,x的取值范围是(0,+∞);
m<-2时,x的取值范围是(m,-2)∪(0,+∞).
14.对于0≤m≤4的m,不等式x2+mx>4x+m-3恒成立,则x的取值范围是 .
答案 x<-1或x>3
解析 ∵x2-4x+3+m(x-1)>0,
即(x-1)(x-3+m)>0对0≤m≤4恒成立,
∴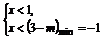 或
或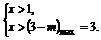
∴x<-1或x>3.
13.已知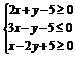 ,则(x+1)2+(y+1)2的最小值和最大值分别是
.
,则(x+1)2+(y+1)2的最小值和最大值分别是
.
答案 13,41
12.(2008·苏中三市质检)若不等式x2-2ax+a>0对x∈R恒成立,则关于t的不等式a2t+1<a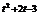 的解集为 .
的解集为 .
答案 (-2,2)
11.若方程x2-2ax+4=0在区间(1,2]上有且仅有一个根,则实数a的取值范围是 .
答案 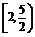
10.(2008·江西文)已知函数f(x)=2x2+(4-m)x+4-m,g(x)=mx,若对于任一实数x,f(x)与g(x)的值至少有一个为正数,则实数m的取值范围是 .
答案 (-∞,4)
9.函数f(x)=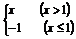 ,则不等式xf(x)-x≤2的解集为
.
,则不等式xf(x)-x≤2的解集为
.
答案 [-1,2]
8.一批救灾物资随26辆汽车从某市以v km/h的速度匀速直达400 km外的灾区,为了安全起见,两辆汽车的间距不得小于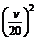 km,则这批物资全部运送到灾区最少需 h.
km,则这批物资全部运送到灾区最少需 h.
答案 10
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com