
5.(2004辽宁)对于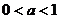 ,给出下列四个不等式
,给出下列四个不等式
①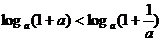 ②
②
③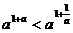 ④
④
其中成立的是_________
4.(2004春北京)已知三个不等式:ab>0,bc-ad>0,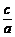 -
- >0(其中a、b、c、d均为实数),用其中两个不等式作为条件,余下的一个不等式作为结论组成一个命题,可组成的正确命题的个数是
>0(其中a、b、c、d均为实数),用其中两个不等式作为条件,余下的一个不等式作为结论组成一个命题,可组成的正确命题的个数是
A.0 B.1 C.2 D.3
3. 对于实数,下命题正确的是 ( )
A.若a<b,则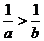 . B.若
. B.若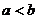 ,则
,则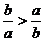 .
.
C.若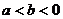 ,则
,则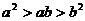 . D.若a>b>0,d>c>0,则
. D.若a>b>0,d>c>0,则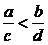
2.(2004北京)已知a、b、c满足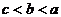 ,且
,且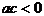 ,那么下列选项中不一定成立的是 ( )
,那么下列选项中不一定成立的是 ( )
A.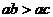 B.
B.
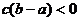 C.
C.  D.
D.

1.(2006春上海) 若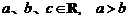 ,则下列不等式成立的是( )
,则下列不等式成立的是( )
A.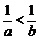 . B.
. B.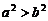 .
C.
.
C. . D.
. D.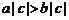 .
.
2.不等式的性质:
(1)对称性: ,
, 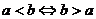
证明:(比较法)
(2)传递性: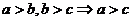 ,
,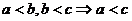
(3)可加性: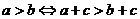 .
.
移项法则: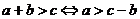
推论:同向不等式可加. 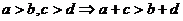
(4)可乘性: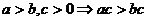 ,
,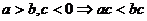
推论1:同向(正)可乘: 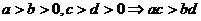
证明:(综合法)
推论2:可乘方(正):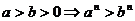
(5) 可开方(正):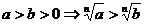
证明:(反证法)
不等式的性质有五个定理,三个推论,一个比较原理,是解、证不等式的基础,对于这些性质,关键是正确理解和熟练运用,要弄清每一个条件和结论,学会对不等式进行条件的放宽和加强
1.比较原理:
两实数之间有且只有以下三个大小关系之一:a>b;a<b;a=b;
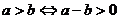 ;
;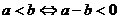 ;
;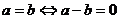 .
.
以此可以比较两个数(式)的大小,--作差比较法.
或作商比较:a>0时,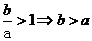 ;a<0时,
;a<0时,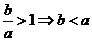 .
.
掌握不等式的性质及其证明,能正确使用这些性质解决一些简单问题
1.已知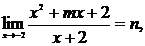 求
求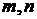
解法一: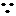
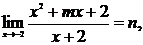
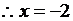 为方程
为方程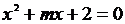 的一根,得
的一根,得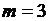 ,代人可得
,代人可得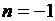
解法二:
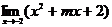 =
=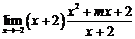
=
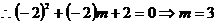 ,代人可得
,代人可得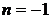
10. 设f(x)是x的三次函数,已知
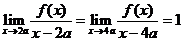 .试求
.试求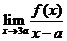 的值,(a为非零常数).
的值,(a为非零常数).
解:由已知可设f(x)=A(x-2a)(x-4a)(x-c),且有
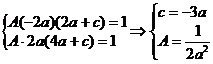
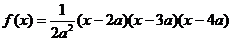
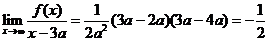
[探索题]在一个以AB为弦的弓形中,C为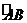 的中点,自A、B分别作弧AB的切线,交于D点,设x为弦AB所对的圆心角,求
的中点,自A、B分别作弧AB的切线,交于D点,设x为弦AB所对的圆心角,求 .
.
解:设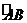 所在圆圆心为O,则C、D、O都在AB的中垂线上,
所在圆圆心为O,则C、D、O都在AB的中垂线上,
∴∠AOD=∠BOD=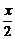 .设OA=r.
.设OA=r.
S△ABC=S四边形AOBC-S△AOB=r2sin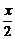 -
-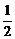 r2sinx=r2sin
r2sinx=r2sin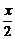 (1-cos
(1-cos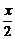 ),
),
S△ABD=S四边形AOBD-S△AOB=r2tan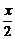 -
-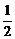 r2sinx=r2
r2sinx=r2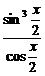 .
.
∴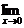
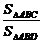 =
=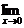
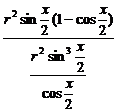 =
=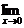
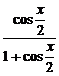 =
=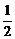 .
.
备题
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com