12.设f(x)＝ax²+bx+c，若6a+2b+c＝0，f(1)·f(3)＞0，

(1)若a＝1，求f(2)的值；

(2)求证：方程f(x)＝0必有两个不等实根x₁、x₂，且3＜x₁+x₂＜5.

解：(1)∵6a+2b+c＝0，a＝1，

∴f(2)＝4a+2b+c＝－2a＝－2.

(2)证明：首先说明a≠0，

∵f(1)·f(3)＝(a+b+c)(9a+3b+c)＝－(5a+b)(3a+b)＞0，

若a＝0，则f(1)·f(3)＝－b²＜0与已知矛盾，

∴a≠0，

其次说明二次方程f(x)＝0必有两个不等实根x₁、x₂，

∵f(2)＝4a+2b+c＝－2a，

∴若a＞0，二次函数f(x)＝ax²+bx+c开口向上，而此时f(2)＜0，

∴若a＜0，二次函数f(x)＝ax²+bx+c开口向下，而此时f(2)＞0.

故二次函数图象必与x轴有两个不同交点，

∴ 二次方程f(x)＝0必有两个不等实根x₁、x₂，

(或利用Δ＝b²－4ac＝b²+4a(6a+2b)＝b²+8ab+24a²＝(b+4a)²+8a²＞0来说明)

∵a≠0，

∴将不等式－(5a+b)(3a+b)＞0两边同除以－a²得

(+3)(+5)＜0，

∴－5＜＜－3.

∴3＜x₁+x₂＝－＜5.

11.不等式(a－2)x²+2(a－2)x－4＜0对一切x∈R恒成立，则a的取值范围是　　.

解析：当a－2＝0，即a＝2时，－4＜0恒成立；

当a－2≠0时，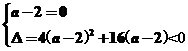　

解之得：－2＜a＜2

∴a的取值范围是－2＜a≤2.

答案：(－2,2]

10.(2009·福建高考)函数f (x)＝ax²+bx+c(a≠0)的图象关于直线x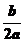＝－对称.据此可推测，对任意的非零实数a，b，c，m，n，p，关于x的方程m[f(x)]²+nf(x)+p＝0的解集都不可能是　　　　　　 　　　　　　　　　　　　　　　　　　　　　(　)

A.{1,2} 　　B.{1,4}　　 C.{1,2,3,4} 　　　D.{1,4,16,64}

解析：设关于f(x)的方程m[f(x)]²+nf(x)+p＝0有两根，即f(x)＝t₁或f(x)＝t₂.

而f(x)＝ax²+bx+c的图象关于x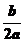＝－对称，因而f(x)＝t₁或f(x)＝t₂的两根也关于x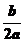＝－对称.而选项D中≠.

答案：D

9.已知f(x)＝x²－2x+3，在闭区间[0，m]上有最大值3，最小值2，则m的取值范围是　　.

解析：若f (x)＝3，则x＝0或x＝2；若f (x)＝2，则x＝1.借助函数图象可知1≤m≤2.

答案：1≤m≤2

8.(2009·天津高考)已知函数f(x)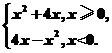＝若f(2－a²)＞f(a)，则实数a的取值范围是　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 (　)

A.(－∞，－1)∪(2，+∞)

B.(－1,2)

C.(－2,1)

D.(－∞，－2)∪(1，+∞)

解析：函数f(x)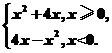＝的图象

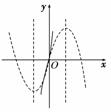如图.

知f(x)在R上为增函数.

∵f(2－a²)＞f(a)，

即2－a²＞a.

解得－2＜a＜1.

答案：C

7.函数f(x)＝4x²－mx+5在区间[－2，+∞)上是增函数，则f(1)的取值范围是　　 (　)

A. f (1)25　 　B.f(1)＝25 　　C. f (1)25 　　　D.f(1)＞25

解析：由题知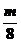≤－2，∴m≤－16.∴f(1)＝9－m25.

答案：A

6.已知二次函数f(x)的二次项系数为a，满足不等式f(x)＞－2x的解集为(1,3)，且方程f(x)+6a＝0有两个相等的实根，求f(x)的解析式.

解：设f(x)＝ax²+bx+c(a≠0).∵f(x)＞－2x，

∴ax²+bx+c＞－2x，即ax²+(b+2)x+c＞0.

∵解集为(1,3)，故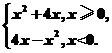

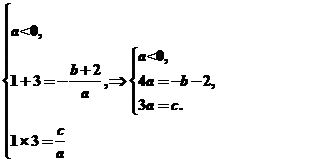
由于f(x)＝－6a有两个相等的实根，故ax²+bx+c+6a＝0中Δ＝0.

∴b²－4a(c+6a)＝0.　　　　　 　　　　　　　③

联立①②③，故a＝－，b＝－，c＝－，

∴f(x)＝－x²－x－.

5.(2010·海口模拟)方程|x²－2x|＝a²+1(a∈(0，+∞))的解的个数是　　　　　　 (　)

A.1个　　　　 B.2个

C.3个　 　　　　　　　D.4个

解析：∵a∈(0，+∞)，∴a²+1＞1，∴y＝|x²－2x|的图象与y＝a²+1的图象总有两个交点，∴方程有两解.故选B.

答案：B

4.已知函数f(x)＝x²+bx+c且f(1+x)＝f (－x)，则下列不等式中成立的是　　　　 (　)

A.f(－2)＜f(0)＜f(2)

B.f(0)＜f (－2)＜f (2)

C. f (0)＜f (2)＜f (－2)

D. f (2)＜f (0)＜f (－2)

解析：∵f (1+x)＝f(－x)，

∴(x+1)²+b(x+1)+c＝x ²－b x+c，

∴x²+(2+b)x+1+b+c＝x²－bx+c，

∴2+b＝－b，即b＝－1，

∴f(x)＝x ²－x+c，其图象的对称轴为x＝，

∴f(0)＜f(2)＜f(－2).

答案：C