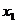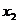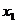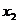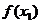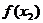3.判断证明函数单调性的一般步骤是：⑴设,是给定区间内的任意两个值，且<；⑵作差－，并将此差式变形(要注意变形的程度)；⑶判断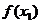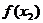－的正负(要注意说理的充分性)；⑷根据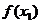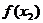－的符号确定其增减性.

2.若函数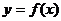在某个区间是增函数或减函数，则就说函数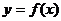在这一区间具有(严格的)单调性，这一区间叫做函数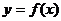的单调区间.此时也说函数是这一区间上的单调函数.

1.对于函数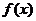的定义域I内某个区间上的任意两个自变量的值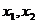

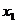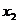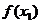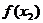⑴若当<时，都有<,则说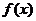在这个区间上是增函数；

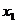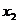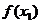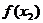⑵若当<时，都有 >,则说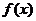在这个区间上是减函数.

7. 已知全集U={1，2，3，4}，A={x|x²-5x+m=0，x∈U}，

求C_UA、m.

解：将x=1、2、3、4代入x²-5x+m=0中，m=4、6.

当m=4时，A={1，4}；

m=6时，A={2，3}.

故满足题条件：C_UA={2，3}，m=4；C_UA={1，4}，m=6.

6. 已知A={0，2，4}，C_UA={-1，1}，C_UB={-1，0，2}，求B=　　

　 利用文恩图，B={1，4}

5. 若S={三角形}，B={锐角三角形}，则C_SB= 　　　　　.

　　 C_SB={直角三角形或钝角三角形}

4.设全集U=﹛1，2，3，4，5﹜，A=﹛2，5﹜，求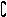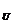A的真子集的个数

3.已知U=﹛(x，y)︱x∈﹛1，2﹜，y∈﹛1，2﹜﹜，

A=﹛(x，y)︱x-y=0﹜，求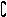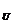A

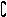
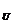(A=﹛(1，2)，(2，1)﹜)

2.设全集U(U≠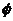)，已知集合M、N、P，且M＝C_UN，N＝C_UP，则M与P的关系是　M＝P　

1.已知S＝{a，b}，A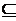S，则A与C_SA的所有组对共有的个数为　　

(A)1　(B)2　(C)3　(D)4　　　　　　 (D)