
8、已知等差数列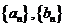 的前 n 项和为
的前 n 项和为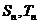 ,若对于任意的自然数
,若对于任意的自然数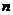 ,都有
,都有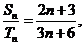 则
则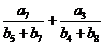 = ▲
= ▲
7、若不等式组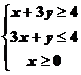
 所表示的平面区域被直线
所表示的平面区域被直线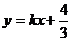 分为面积相等的两部分,则k的值是 ▲
分为面积相等的两部分,则k的值是 ▲
6、若函数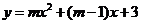 在
在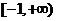 上为减函数,则实数
上为减函数,则实数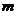 的取值范围为 ▲
的取值范围为 ▲
5、已知命题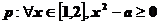 ,命题
,命题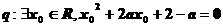 ,若命题 “
,若命题 “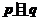 ”是真命题,则实数
”是真命题,则实数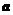 的取值范围是 ▲
的取值范围是 ▲
4、若复数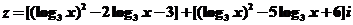 是纯虚数(
是纯虚数(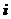 为虚数单位),则实数
为虚数单位),则实数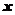 =_______▲______.
=_______▲______.
3、设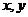 是满足
是满足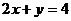 的正数,则
的正数,则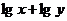 的最大值是
▲
.
的最大值是
▲
.
2、不等式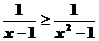 的解集为
▲
的解集为
▲
1、已知集合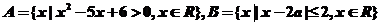 ,若
,若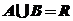 ,则实数
,则实数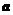 的取值范围是______▲_____.
的取值范围是______▲_____.
2.复合函数单调性的判断
对于函数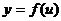 和
和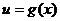 ,如果
,如果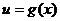 在区间
在区间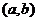 上是具有单调性,当
上是具有单调性,当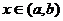 时,
时,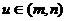 ,且
,且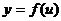 在区间
在区间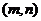 上也具有单调性,则复合函数
上也具有单调性,则复合函数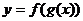 在区间
在区间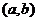 具有单调性的规律见下表:
具有单调性的规律见下表:
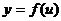 |
增 ↗ |
减 ↘ |
||
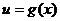 |
增 ↗ |
减 ↘ |
增 ↗ |
减 ↘ |
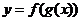 |
增 ↗ |
减 ↘ |
减 ↘ |
增 ↗ |
以上规律还可总结为:“同向得增,异向得减”或“同增异减”.
证明:①设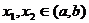 ,且
,且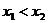
∵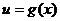 在
在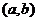 上是增函数,
上是增函数,
∴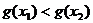 ,且
,且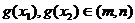
∵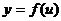 在
在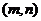 上是增函数,∴
上是增函数,∴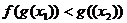 .
.
所以复合函数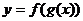 在区间
在区间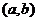 上是增函数
上是增函数
②设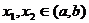 ,且
,且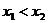 ,∵
,∵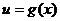 在
在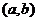 上是增函数,
上是增函数,
∴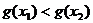 ,且
,且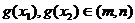
∵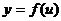 在
在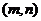 上是减函数,∴
上是减函数,∴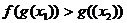 .
.
所以复合函数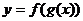 在区间
在区间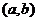 上是减函数
上是减函数
③设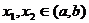 ,且
,且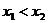 ,∵
,∵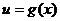 在
在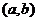 上是减函数,
上是减函数,
∴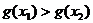 ,且
,且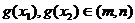
∵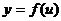 在
在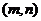 上是增函数,∴
上是增函数,∴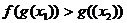 .
.
所以复合函数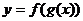 在区间
在区间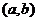 上是减函数
上是减函数
④设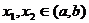 ,且
,且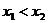 ,∵
,∵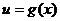 在
在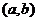 上是减函数,
上是减函数,
∴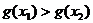 ,且
,且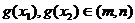
∵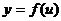 在
在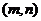 上是减函数,∴
上是减函数,∴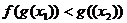 .
.
所以复合函数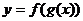 在区间
在区间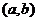 上是增函数
上是增函数
例2.求函数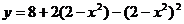 的值域,并写出其单调区间
的值域,并写出其单调区间
解:题设函数由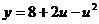 和
和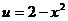 复合而成的复合函数,
复合而成的复合函数,
函数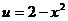 的值域是
的值域是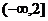 ,
,
在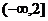 上
上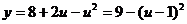 的值域是
的值域是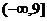 .
.
故函数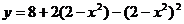 的值域是
的值域是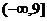 .
.
对于函数的单调性,不难知二次函数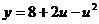 在区间
在区间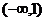 上是减函数,在区间
上是减函数,在区间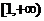 上是增函数;
上是增函数;
二次函数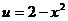 区间
区间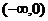 上是减函数,在区间
上是减函数,在区间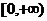 上是增函数
上是增函数
当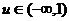 时,
时,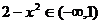 ,即
,即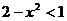 ,
,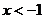 或
或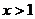 .
.
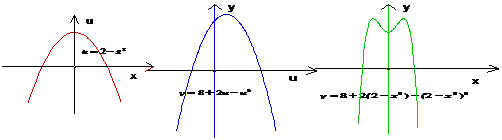 当
当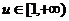 时,
时,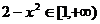 ,即
,即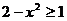 ,
,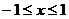 .
.
因此,本题应在四个区间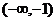 ,
,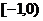 ,
,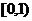 ,
,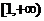 上考虑
上考虑
① 当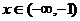 时,
时,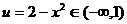 ,
,
而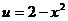 在
在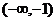 上是增函数,
上是增函数,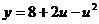 在
在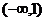 上是增函数,所以,函数
上是增函数,所以,函数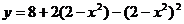 在区间
在区间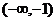 上是增函数
上是增函数
②当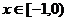 时,
时,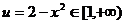 ,
,
而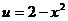 在
在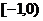 上是增函数,
上是增函数,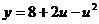 在
在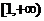 上是减函数,
上是减函数,
所以,函数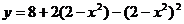 在区间
在区间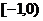 上是减函数
上是减函数
③当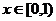 时,
时,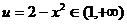 ,
,
而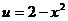 在
在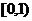 上是减函数,
上是减函数,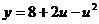 在
在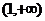 上是减函数,
上是减函数,
所以,函数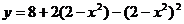 在区间
在区间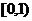 上是增函数
上是增函数
④当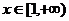 时,
时,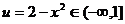 ,
,
而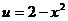 在
在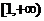 上是增函数,
上是增函数,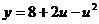 在
在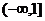 上是减函数,所以,函数
上是减函数,所以,函数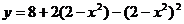 在区间
在区间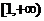 上是减函数
上是减函数
综上所述,函数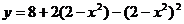 在区间
在区间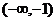 、
、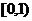 上是增函数;在区间
上是增函数;在区间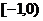 、
、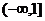 上是减函数
上是减函数
另外,本题给出的复合函数是偶函数,在讨论具有奇偶性的函数的单调性时,应注意应用其奇函数或偶函数的性质,以使解题过程简捷、清楚、具有条理性
1.函数单调性的证明
例1.判断并证明函数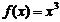 的单调性
的单调性
证明:设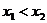 则
则
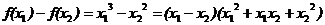
∵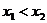 ∴
∴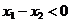 ,
,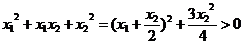 ,
,
∴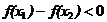 即
即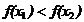 (注:关键
(注:关键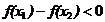 的判断)
的判断)
∴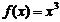 在R上是增函数.
在R上是增函数.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com