
10.如图所示,已知正方形ABCD和矩形ACEF所在的平面互相垂直,AB=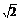 ,AF=1,M是线段EF的中点.
,AF=1,M是线段EF的中点.
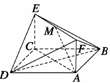 求证:
求证:
(1)AM∥平面BDE;
(2)AM⊥平面BDF.
证明 (1)建立如图所示的空间直角坐标系,
设AC∩BD=N,连接NE.
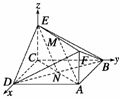 则点N、E的坐标分别为
则点N、E的坐标分别为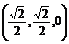 、(0,0,1).
、(0,0,1).
∴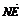 =
=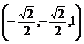 .
.
又点A、M的坐标分别是
(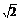 ,
,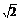 ,0)、
,0)、 ,
,
∴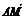 =
=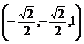 .
.
∴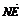 =
=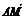 且NE与AM不共线.∴NE∥AM.
且NE与AM不共线.∴NE∥AM.
又∵NE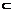 平面BDE,AM
平面BDE,AM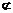 平面BDE,
平面BDE,
∴AM∥平面BDE.
(2)由(1)知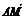 =
=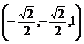 ,
,
∵D(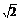 ,0,0),F(
,0,0),F(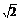 ,
,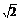 ,1),∴
,1),∴ =(0,
=(0,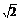 ,1).
,1).
∴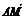 ·
· =0.∴
=0.∴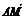 ⊥
⊥ .
.
同理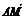 ⊥
⊥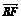 .又DF∩BF=F,∴AM⊥平面BDF.
.又DF∩BF=F,∴AM⊥平面BDF.
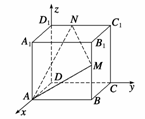
9.已知正方体ABCD-A1B1C1D1中,M、N分别为BB1、C1D1的中点,建立适当的坐标系,求平面AMN的法向量.
解 以D为原点,DA、DC、DD1所在直线为坐标轴建立空间直角坐标系.(如图所示).
设棱长为1,则A(1,0,0),M(1,1,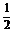 ),N(0,
),N(0,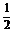 ,1).
,1).
∴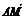 =(0,1,
=(0,1,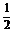 ),
),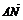 =(-1,
=(-1,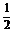 ,1).
,1).
 设平面AMN的法向量n=(x,y,z)
设平面AMN的法向量n=(x,y,z)
∴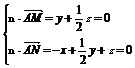
令y=2,∴x=-3,z=-4.∴n=(-3,2,-4).
∴(-3,2,-4)为平面AMN的一个法向量.
8.若|a|=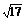 ,b=(1,2,-2),c=(2,3,6),且a⊥b,a⊥c,则a=
.
,b=(1,2,-2),c=(2,3,6),且a⊥b,a⊥c,则a=
.
答案 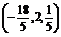 或
或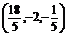
7.若A(0,2,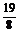 ),B(1,-1,
),B(1,-1,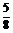 ),C(-2,1,
),C(-2,1,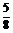 )是平面
)是平面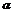 内三点,设平面
内三点,设平面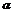 的法向量a=(x,y,z),则x∶y∶z= .
的法向量a=(x,y,z),则x∶y∶z= .
答案 2∶3∶(-4)
6.下列四个正方体图形中,A、B为正方体的两个顶点,M、N、P分别为其所在棱的中点,能得出AB∥平面MNP的图形的序号是 .
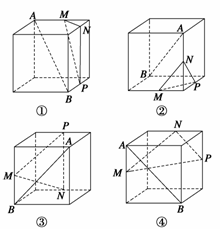
答案 ①④
5.设点C(2a+1,a+1,2)在点P(2,0,0)、A(1,-3,2)、B(8,-1,4)确定的平面上,则a= .
答案 16
4.已知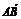 =(1,5,-2),
=(1,5,-2), =(3,1,z),若
=(3,1,z),若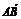 ⊥
⊥ ,
,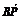 =(x-1,y,-3),且
=(x-1,y,-3),且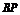 ⊥平面ABC,则实数x,y,z分别为 .
⊥平面ABC,则实数x,y,z分别为 .
答案 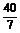 ,-
,-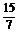 ,4
,4
3.已知A(1,0,0)、B(0,1,0)、C(0,0,1),则平面ABC的一个单位法向量是 (写出一个即可).
答案 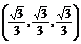
2.已知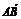 =(2,4,5),
=(2,4,5),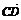 =(3,x,y),若
=(3,x,y),若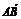 ∥
∥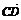 ,则x=
,y=
.
,则x=
,y=
.
答案 6 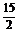
1.若平面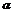 、
、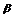 的法向量分别为n1=(2,3,5),n2=(-3,1,-4),则
的法向量分别为n1=(2,3,5),n2=(-3,1,-4),则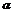 ,
, 的位置关系是 (用“平行”,“垂直”,“相交但不垂直”填空).
的位置关系是 (用“平行”,“垂直”,“相交但不垂直”填空).
答案 相交但不垂直
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com