
19.(本小题满分16分)已知数列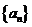 的首项为
的首项为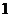 ,
,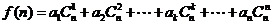
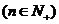 .
.
(1)若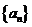 为常数列,求
为常数列,求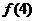 的值;
的值;
(2)若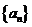 为公比为
为公比为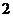 的等比数列,求
的等比数列,求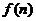 的解析式;
的解析式;
(3)数列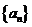 能否成等差数列,使得
能否成等差数列,使得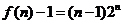 对一切
对一切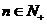 都成立.若能,求出数列
都成立.若能,求出数列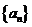 的通项公式;若不能,试说明理由.
的通项公式;若不能,试说明理由.
18.(本小题满分16分)已知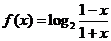
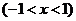 .
.
(1)若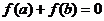 ,求证:
,求证: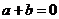 ;
;
(2)设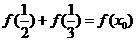 ,求
,求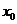 的值;
的值;
(3)设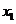 、
、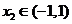 ,是否存在
,是否存在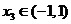 ,使得
,使得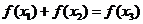 ,若存在,求出
,若存在,求出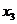 ,并证明你的结论;若不存在,请说明理由.
,并证明你的结论;若不存在,请说明理由.
17.(本小题满分14分)某游乐场举办“迎国庆”有奖射击活动,规定参与者每人射击三次,三次全中,奖励价值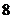 元的小礼品;中两次且连中,奖励价值
元的小礼品;中两次且连中,奖励价值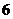 元的小礼品;中两次但不连中,奖励价值
元的小礼品;中两次但不连中,奖励价值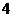 元的小礼品;只中一次,奖励价值
元的小礼品;只中一次,奖励价值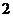 元的小礼品;不中的则没有奖品.设某人射击一次中靶的概率为
元的小礼品;不中的则没有奖品.设某人射击一次中靶的概率为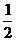 ,用
,用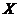 表示获得奖品的金额数.
表示获得奖品的金额数.
(1)求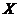 的概率分布表;
的概率分布表;
(2)求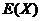 .
.
16.(本题满分14分)在直角坐标系中以原点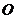 为极点,
为极点,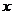 轴的正半轴为极轴建立极坐标系,且在两种坐标系中取相同的长度单位.已知圆
轴的正半轴为极轴建立极坐标系,且在两种坐标系中取相同的长度单位.已知圆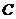 的圆心的极坐标
的圆心的极坐标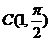 ,半径
,半径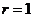 ,直线
,直线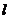 的参数方程为
的参数方程为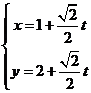 (
(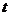 为参数).
为参数).
(1)求圆的极坐标方程,并将极坐标方程化成直角坐标方程;
(2)将直线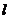 的参数方程化为普通方程,并判断直线
的参数方程化为普通方程,并判断直线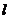 与圆
与圆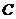 的位置关系.
的位置关系.
15.(本题满分14分)已知复数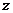 满足
满足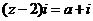
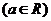 .
.
(1)求复数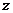 ;(2)
;(2)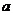 为何值时,复数
为何值时,复数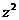 对应点在第一象限.
对应点在第一象限.
14.一袋中装有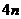 只红球和
只红球和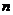 只黑球(所有球的形状、大小都相同),每一次从袋中摸出两只球,且每次摸球后均放回袋中. 现规定:摸出的两只球颜色不同则为中奖.设三次摸球恰有一次中奖的概率为
只黑球(所有球的形状、大小都相同),每一次从袋中摸出两只球,且每次摸球后均放回袋中. 现规定:摸出的两只球颜色不同则为中奖.设三次摸球恰有一次中奖的概率为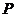 ,则当
,则当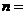 ▲ 时,使得
▲ 时,使得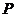 最大.
最大.
13.已知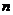 是给定的正整数,整数
是给定的正整数,整数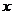 、
、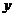 满足不等式
满足不等式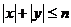 ,则整数对
,则整数对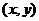 的个数为
的个数为
▲ .

12.连续3次抛掷一枚质地均匀的硬币,在至少有一次出现正面向上的条件下,恰有一次出现反面向上的概率为 ▲ .
11.在平面直角坐标系中,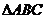 的顶点
的顶点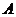 、
、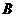 分别是离心率为
分别是离心率为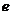 的圆锥曲线
的圆锥曲线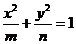 的焦点,顶点
的焦点,顶点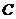 在该曲线上.一同学已正确地推得:当
在该曲线上.一同学已正确地推得:当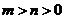 时,有
时,有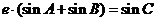 .类似地,当
.类似地,当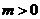 、
、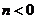 时,有
时,有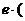 ▲
▲ 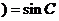 .
. 
10.定义在实数集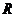 上的函数
上的函数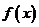 满足
满足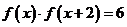 ,若
,若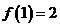 ,则
,则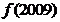 的值为 ▲ .
的值为 ▲ .
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com