
22. Just because they make more money than I do, _______ they seem to look down on me.
A. so B. and C. but D. 不填
第一节 单项填空(共15小题;每小题1分,满分15分)
从A、B、C、D四个选项中,选出可以填入空白处的最佳选项。
21. He suggested the problem worth paying attention _______ at the meeting.
A. to be discussed B. to discussing C. to discuss D. to being discussed
21.本小题主要考察函数、函数的导数和不等式等基础知识,考察综合运用数学知识进行推理论证的能力和份额类讨论的思想(满分14分)
(I)解: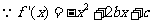 ,由
,由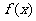 在
在 处有极值
处有极值
可得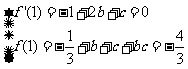
解得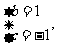 或
或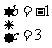
若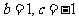 ,则
,则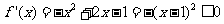 ,此时
,此时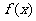 没有极值;
没有极值;
若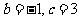 ,则
,则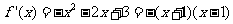
当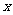 变化时,
变化时,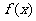 ,
,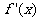 的变化情况如下表:
的变化情况如下表:
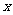 |
 |
 |
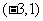 |
1 |
 |
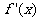 |
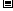 |
0 |
+ |
0 |
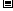 |
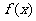 |
 |
极小值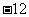 |
 |
极大值 |
 |
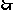 当
当 时,
时,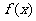 有极大值
有极大值 ,故
,故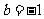 ,
,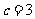 即为所求。
即为所求。
(Ⅱ)证法1: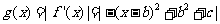
当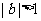 时,函数
时,函数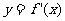 的对称轴
的对称轴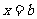 位于区间
位于区间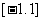 之外。
之外。
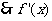 在
在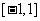 上的最值在两端点处取得
上的最值在两端点处取得
故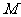 应是
应是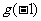 和
和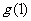 中较大的一个
中较大的一个
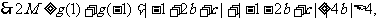 即
即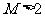
证法2(反证法):因为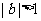 ,所以函数
,所以函数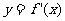 的对称轴
的对称轴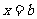 位于区间
位于区间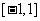 之外,
之外,
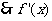 在
在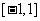 上的最值在两端点处取得。
上的最值在两端点处取得。
故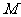 应是
应是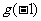 和
和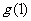 中较大的一个
中较大的一个
假设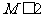 ,则
,则
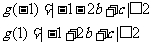


将上述两式相加得:
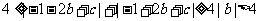 ,导致矛盾,
,导致矛盾,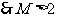
(Ⅲ)解法1: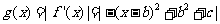
(1)当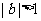 时,由(Ⅱ)可知
时,由(Ⅱ)可知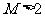 ;
;
(2)当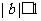 时,函数
时,函数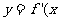 )的对称轴
)的对称轴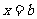 位于区间
位于区间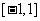 内,
内, 

此时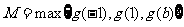
由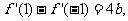 有
有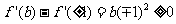
①若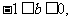 则
则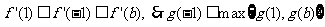 ,
,
于是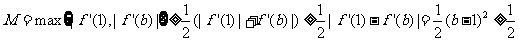
②若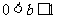 ,则
,则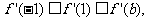
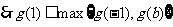
于是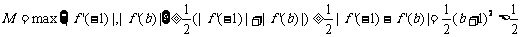
综上,对任意的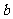 、
、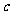 都有
都有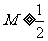
而当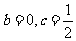 时,
时,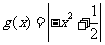 在区间
在区间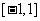 上的最大值
上的最大值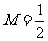
故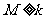 对任意的
对任意的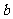 、
、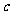 恒成立的
恒成立的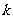 的最大值为
的最大值为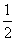 。
。
解法2: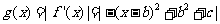
(1)当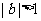 时,由(Ⅱ)可知
时,由(Ⅱ)可知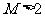 ;
; 

(2)当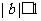 时,函数
时,函数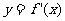 的对称轴
的对称轴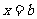 位于区间
位于区间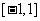 内,
内,
此时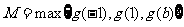
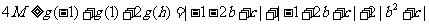


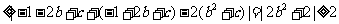 ,即
,即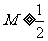
下同解法1
21.(本小题满分14分) 

已知关于x的函数f(x)=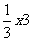 +bx2+cx+bc,其导函数为f+(x).令g(x)=∣f+(x) ∣,记函数g(x)在区间[-1、1]上的最大值为M.
+bx2+cx+bc,其导函数为f+(x).令g(x)=∣f+(x) ∣,记函数g(x)在区间[-1、1]上的最大值为M.
(Ⅰ)如果函数f(x)在x=1处有极值- ,试确定b、c的值:
,试确定b、c的值:
(Ⅱ)若∣b∣>1,证明对任意的c,都有M>2:


(Ⅲ)若M≧K对任意的b、c恒成立,试求k的最大值。
20.(本小题满分13分)
如图,过抛物线y2=2PX(P>0)的焦点F的直线与抛物线相交于M、N两点,自M、N向准线L作垂线,垂足分别为M1、N1
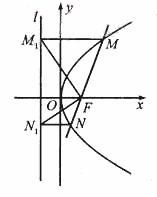 (Ⅰ)求证:FM1⊥FN1:
(Ⅰ)求证:FM1⊥FN1:
(Ⅱ)记△FMM1、、△FM1N1、△FN N1的面积分别为S1、、S2、,S3,试判断S22=4S1S3是否成立,并证明你的结论。 

20题。本小题主要考查抛物线的概念,抛物线的几何性质等平面解析几何的基础知识,考查综合运用数学知识进行推理运算的能力(满分13分)
(1) 证法1:由抛物线的定义得
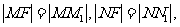


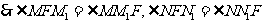 2分
2分
 如图,设准线l与x的交点为
如图,设准线l与x的交点为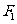
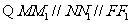
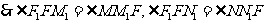
而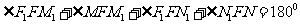
即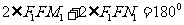

故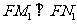
证法2:依题意,焦点为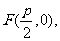 准线l的方程为
准线l的方程为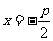
设点M,N的坐标分别为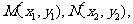 直线MN的方程为
直线MN的方程为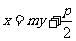 ,则有
,则有
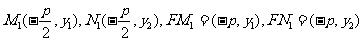
由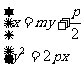 得
得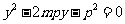
于是,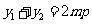 ,
,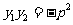
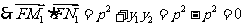 ,故
,故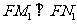
(Ⅱ)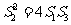 成立,证明如下:
成立,证明如下:
证法1:设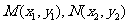 ,则由抛物线的定义得
,则由抛物线的定义得
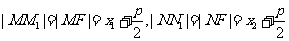 ,于是
,于是
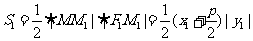
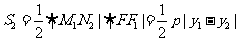

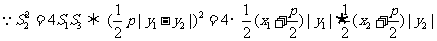
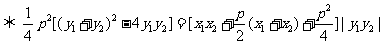
将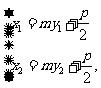 与
与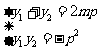 代入上式化简可得
代入上式化简可得 

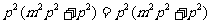 ,此式恒成立。
,此式恒成立。
故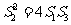 成立。
成立。
证法2:如图,设直线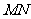 M的倾角为
M的倾角为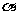 ,
,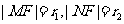
则由抛物线的定义得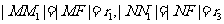
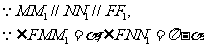
于是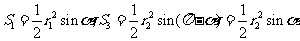
在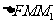 和
和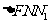 中,由余弦定理可得
中,由余弦定理可得

由(I)的结论,得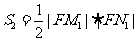
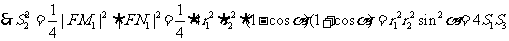
即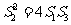 ,得证。
,得证。
19.(本小题满分12分)
已知{an}是一个公差大于0的等差数列,且满足a3a6=55, a2+a7=16.
(Ⅰ)求数列{an}的通项公式:
(Ⅱ)若数列{an}和数列{bn}满足等式:an==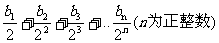 ,求数列{bn}的前n项和Sn
,求数列{bn}的前n项和Sn 

解(1)解:设等差数列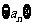 的公差为d,则依题设d>0
的公差为d,则依题设d>0 

由a2+a7=16.得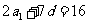 ①
①
由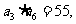 得
得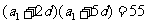 ②
②
由①得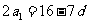 将其代入②得
将其代入②得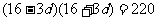 。即
。即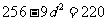
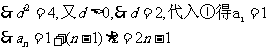


(2)令
两式 相减得
相减得
于是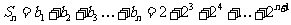
= -4=
-4=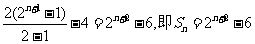
18. 本小题主要考察空间直线与直线、直线与平面的位置关系和二面角等基础知识,考查空间想象能力、推理论证能力和运算求解能力。(满分12分)
(Ⅰ)证发1:连接BD,由底面是正方形可得AC BD。
BD。
 SD
SD 平面ABCD,
平面ABCD,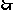 BD是BE在平面ABCD上的射影,
BD是BE在平面ABCD上的射影,
由三垂线定理得AC BE.
BE.
(II)解法1: SD
SD 平面ABCD,CD
平面ABCD,CD 平面ABCD,
平面ABCD,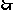 SD
SD CD.
CD.
又底面ABCD是正方形,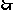 CD
CD AD,又SD
AD,又SD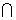 AD=D,
AD=D,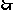 CD
CD 平面SAD。
平面SAD。
过点D在平面SAD内做DF AE于F,连接CF,则CF
AE于F,连接CF,则CF AE,
AE,
故 CFD是二面角C-AE-D 的平面角,即
CFD是二面角C-AE-D 的平面角,即 CFD=60°
CFD=60°
在Rt△ADE中, AD=
AD=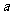 , DE=
, DE= 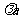 , AE=
, AE=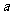
 。
。
于是,DF=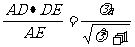
在Rt△CDF中,由 cot60°=
cot60°=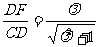
 得
得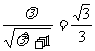 , 即
, 即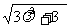 =3
=3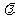


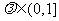 , 解得
, 解得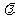 =
=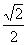
18. (本小题满分12分)
 如图,四棱锥S=ABCD的底面是正方形,SD⊥平面ABCD,SD=AD=a,点E是SD上的点,且DE=
如图,四棱锥S=ABCD的底面是正方形,SD⊥平面ABCD,SD=AD=a,点E是SD上的点,且DE=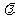 a(0<
a(0<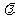 ≦1).
≦1). 

(Ⅰ)求证:对任意的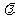
 (0、1),都有AC⊥BE:
(0、1),都有AC⊥BE:
(Ⅱ)若二面角C-AE-D的大小为600C,求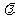 的值。
的值。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com