
7. 定义在R上的函数f(x)满足f(x)= 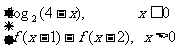 ,则f(3)的值为( B )
,则f(3)的值为( B )
A.-1
B. -2
C.1
D. 2. 

6. 函数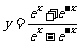 的图像大致为( A ).
的图像大致为( A ).


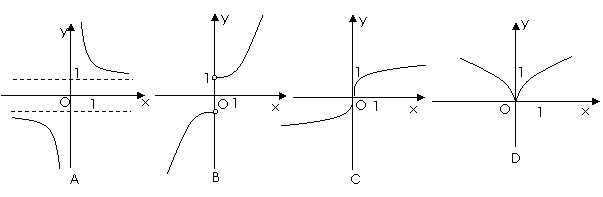
5.在R上定义运算⊙:  ⊙
⊙ ,则满足
,则满足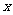 ⊙
⊙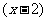 <0的实数
<0的实数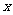 的取值范围为( B ).
的取值范围为( B ).
 A.(0,2)
B.(-2,1) C.
A.(0,2)
B.(-2,1) C.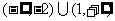 D.(-1,2)
D.(-1,2) 

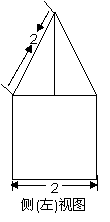
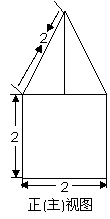
4. 一空间几何体的三视图如图所示,则该几何体的体积为( C ).
A.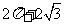 B.
B. 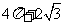 C.
C.
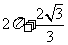 D.
D.
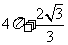
3.将函数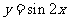 的图象向左平移
的图象向左平移 个单位, 再向上平移1个单位,所得图象的函数解析式是( A).
个单位, 再向上平移1个单位,所得图象的函数解析式是( A).


A. 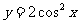 B.
B. 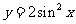 C.
C.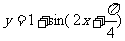 D.
D. 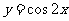
[命题立意]:本题考查三角函数的图象的平移和利用诱导公式及二倍角公式进行化简解析式的基本知识和基本技能,学会公式的变形.
2.复数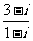 等于(C ).
等于(C ).
A. B.
B.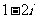 C.
C.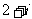 D.
D.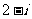
1.集合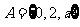 ,
,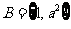 ,若
,若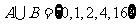 ,则
,则 的值为( D )
的值为( D )
A.0 B.1 C.2 D.4
21、解:(I)已知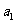 是奇数,假设
是奇数,假设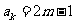 是奇数,其中
是奇数,其中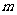 为正整数,
为正整数,
则由递推关系得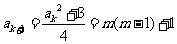 是奇数。
是奇数。 

根据数学归纳法,对任何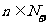 ,
,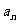 都是奇数。
都是奇数。
(II)(方法一)由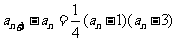 知,
知,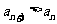 当且仅当
当且仅当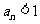 或
或 。
。
另一方面,若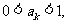 则
则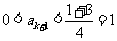 ;若
;若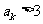 ,则
,则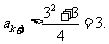
根据数学归纳法,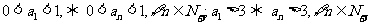
综合所述,对一切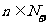 都有
都有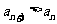 的充要条件是
的充要条件是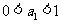 或
或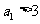 。
。
(方法二)由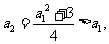 得
得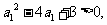 于是
于是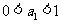 或
或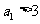 。
。
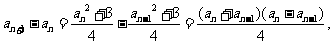


因为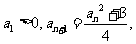 所以所有的
所以所有的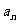 均大于0,因此
均大于0,因此 与
与 同号。
同号。
根据数学归纳法, ,
, 与
与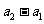 同号。
同号。
因此,对一切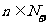 都有
都有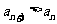 的充要条件是
的充要条件是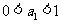 或
或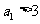 。
。


20、解:本小题主要考查直线和椭圆的标准方程和参数方程,直线和曲线的几何性质,等比数列等基础知识。考查综合运用知识分析问题、解决问题的能力。本小题满分13分。
解:(I)(方法一)由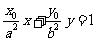 得
得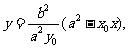 代入椭圆
代入椭圆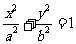 ,
,
得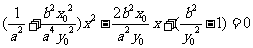 .
.
将 代入上式,得
代入上式,得 从而
从而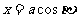
因此,方程组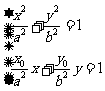 有唯一解
有唯一解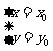 ,即直线
,即直线 与椭圆有唯一交点P.
与椭圆有唯一交点P. 

(方法二)显然P是椭圆与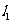 的交点,若Q
的交点,若Q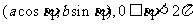 是椭圆与
是椭圆与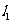 的交点,代入
的交点,代入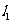 的方程
的方程 ,得
,得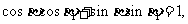
即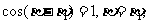 故P与Q重合。
故P与Q重合。
(方法三)在第一象限内,由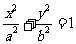 可得
可得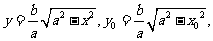
椭圆在点P处的切线斜率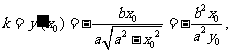
切线方程为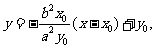 即
即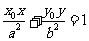 。
。
因此,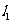 就是椭圆在点P处的切线。
就是椭圆在点P处的切线。
根据椭圆切线的性质,P是椭圆与直线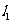 的唯一交点。
的唯一交点。
(II)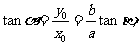
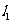 的斜率为
的斜率为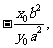
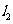 的斜率为
的斜率为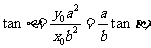
由此得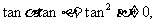
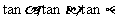 构成等比数列。
构成等比数列。
19、解: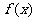 的定义域是(0,+
的定义域是(0,+ ),
),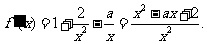
设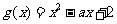 ,二次方程
,二次方程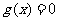 的判别式
的判别式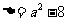 .
.
①
当 ,即
,即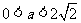 时,对一切
时,对一切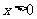 都有
都有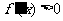 ,此时
,此时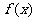 在
在 上是增函数。
上是增函数。
②
当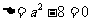 ,即
,即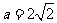 时,仅对
时,仅对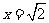 有
有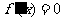 ,对其余的
,对其余的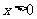 都有
都有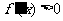 ,此时
,此时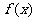 在
在 上也是增函数。
上也是增函数。
③
当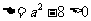 ,即
,即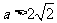 时,
时, 

方程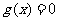 有两个不同的实根
有两个不同的实根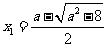 ,
, ,
, .
.
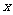 |
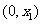 |
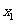 |
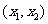 |
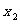 |
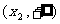 |
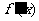 |
+ |
0 |
_ |
0 |
+ |
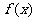 |
单调递增 |
极大 |
单调递减 |
极小 |
单调递增 |
此时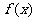 在
在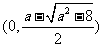 上单调递增, 在
上单调递增, 在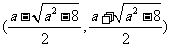 是上单调递减, 在
是上单调递减, 在 上单调递增.
上单调递增.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com