
(11)若随机变量X~N(μ,σ2),则P(X≤μ)= .
(12)以直角坐标系的原点为极点,x轴的正半轴为极轴, 

并在两种坐标系中取相同的长度单位,已知直线的
 极坐标方程为
极坐标方程为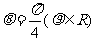 ,它与曲线
,它与曲线


(α为参数)相交于两点A和B,则

|AB|= .
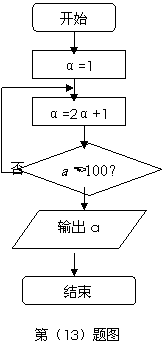
(13)程序框图(即算法流程图)如图所示,其输出结果是
.
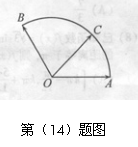
(14)给定两个长度为1的平面向量 和
和 ,它们的夹
,它们的夹
角为120°.如图所示,点C在以O为圆心的圆弧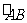
上变动.若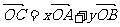 ,其中
,其中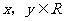 ,则x+y
,则x+y
的最大值是 .
 (15)对于四面体ABCD,下列命题正确的是
(15)对于四面体ABCD,下列命题正确的是
(写出所有正确命题的编号).
①相对棱AB与CD所在的直线异面;
②由顶点A作四面体的高,其垂足是△BCD三条高线的交点;
③若分别作△ABC和△ABD的边AB上的高,则这两条高所在的直线异面;
④分别作三组相对棱中点的连线,所得的三条线段相交于一点;
⑤最长棱必有某个端点,由它引出的另两条棱的长度之和大于最长棱.
(1)i是虚数单位,若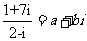 (a、b∈R),则乘积ab的值是
(a、b∈R),则乘积ab的值是
(A)-15 (B)-3 (C)3 (D)15
(2)若集合A={x|︱2x-1︱<3},B={x|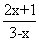 <0},则A∩B是
<0},则A∩B是
(A){x|-1<x<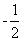 或2<x<3}
(B){x|2<x<3}
或2<x<3}
(B){x|2<x<3}
(C){x|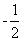 <x<2}
(D){x|-1<x<
<x<2}
(D){x|-1<x<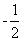 }
}
 (3)下列曲线中离心率为
(3)下列曲线中离心率为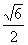 的是
的是
(A)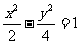 (B)
(B)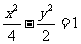
(C)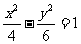 (D)
(D)

(4)下列选项中,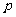 是
是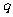 的必要不充分条件的是
的必要不充分条件的是
(A)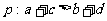 ,
, 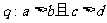
(B)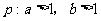 ,
, 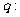
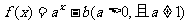 的图像不过第二象限
的图像不过第二象限
(C)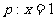 ,
,
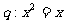
(D)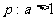 ,
,
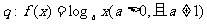 在
在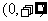 上为增函数
上为增函数
(5)已知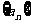 为等差数列,
为等差数列,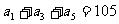 ,
,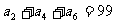 。以
。以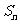 表示
表示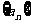 的前n项和,则使得
的前n项和,则使得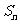 达到最大值的n是
达到最大值的n是
(A)21 (B)20 (C)19 (D)18
(6)设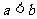 ,函数
,函数 的图像可能是
的图像可能是
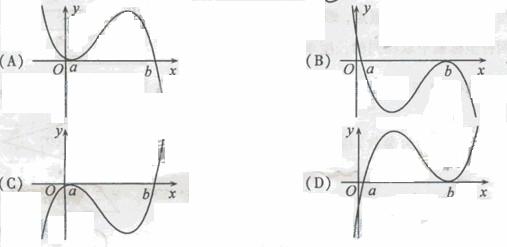
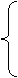
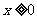
(7)若不等式组
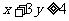 所表示的平面区域被直线
所表示的平面区域被直线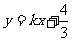 分为面积相等的两
分为面积相等的两
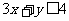
部分,则k的值是
(A) (B)
(B)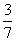 (C)
(C)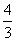 (D)
(D)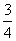
(8)已知函数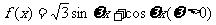 ,
,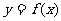 的图像与直线
的图像与直线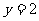 的两个相邻交点的距离等于
的两个相邻交点的距离等于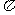 ,则
,则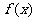 的单调递增区间是
的单调递增区间是
(A)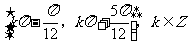 (B)
(B)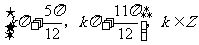
(C)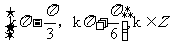 (D)
(D)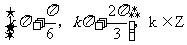
(9)已知函数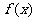 在R上满足
在R上满足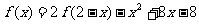 ,则曲线
,则曲线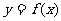 在点
在点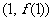 处的切线方程是
处的切线方程是
(A)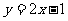
 (B)
(B)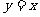 (C)
(C)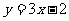 (D)
(D)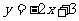
(10)考察正方体6个面的中心,甲从这6个点中任意选两个点连成直线,乙也从这6个点种任意选两个点连成直线,则所得的两条直线相互平行但不重合的概率等于
(A)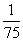 (B)
(B) (C)
(C)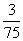 (D)
(D)
(在此卷上答题无效)
2009年普通高等学校招生全国统一考试(安徽卷)
数 学(理科)
第Ⅱ卷(非选择题 共100分)
请用0.5毫米黑色墨水签字笔在答题卡上作答,在试题卷上答题无效.
(17)(本小题满分12分)
为了测量两山顶M,N间的距离,飞机沿水平方向在A,B两点进行测量,A,B,M,N在同一个铅垂平面内(如示意图),飞机能够测量的数据有俯角和A,B间的距离,请设计一个方案,包括:①指出需要测量的数据(用字母表示,并在图中标出);②用文字和公式写出计算M,N间的距离的步骤。
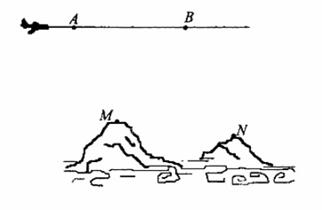
(17) 解:
方案一:①需要测量的数据有:A
点到M,N点的俯角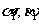 ;B点到M,
;B点到M,
N的俯角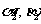 ;A,B的距离 d (如图)
;A,B的距离 d (如图)
所示) . ……….3分
②第一步:计算AM . 由正弦定理 ;
;
第二步:计算AN . 由正弦定理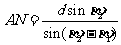 ;
;
第三步:计算MN. 由余弦定理 .
.
方案二:①需要测量的数据有:
A点到M,N点的俯角 ,
,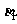 ;B点到M,N点的府角
;B点到M,N点的府角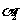 ,
,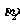 ;A,B的距离 d (如图所示).
;A,B的距离 d (如图所示).
②第一步:计算BM . 由正弦定理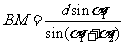 ;
;
第二步:计算BN . 由正弦定理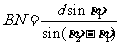 ;
;
第三步:计算MN . 由余弦定理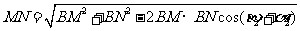
(18)(本小题满分12分)
某工厂有工人1000名, 其中250名工人参加过短期培训(称为A类工人),另外750名工人参加过长期培训(称为B类工人),现用分层抽样方法(按A类、B类分二层)从该工厂的工人中共抽查100名工人,调查他们的生产能力(此处生产能力指一天加工的零件数)。
(I)求甲、乙两工人都被抽到的概率,其中甲为A类工人,乙为B类工人;
(II)从A类工人中的抽查结果和从B类工人中的抽插结果分别如下表1和表2.
表1:
|
生产能力分组 |
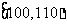 |
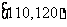 |
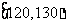 |
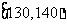 |
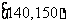 |
|
人数 |
4 |
8 |
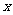 |
5 |
3 |
表2:
|
生产能力分组 |
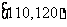 |
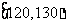 |
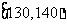 |
 |
|
人数 |
6 |
y |
36 |
18 |
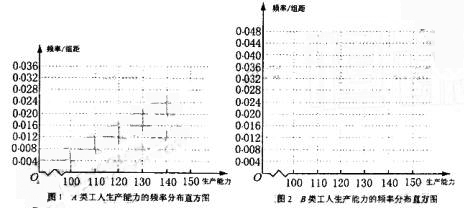
(i)先确定x,y,再在答题纸上完成下列频率分布直方图。就生产能力而言,A类工人中个体间的差异程度与B类工人中个体间的差异程度哪个更小?(不用计算,可通过观察直方图直接回答结论)
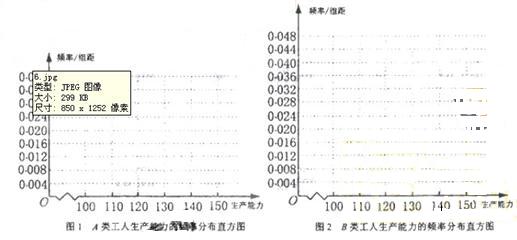
(ii)分别估计A类工人和B类工人生产能力的平均数,并估计该工厂工人的生产能力的平均数,同一组中的数据用该组区间的中点值作代表)
(18) 解:
(Ⅰ)甲、乙被抽到的概率均为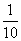 ,且事件“甲工人被抽到”与事件“乙工人被抽到”相互独立,故甲、乙两工人都被抽到的概率为
,且事件“甲工人被抽到”与事件“乙工人被抽到”相互独立,故甲、乙两工人都被抽到的概率为
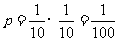 .
.
(Ⅱ)(i)由题意知A类工人中应抽查25名,B类工人中应抽查75名.
故 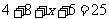 ,得
,得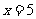 ,
,
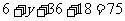 ,得
,得 .
.
频率分布直方图如下
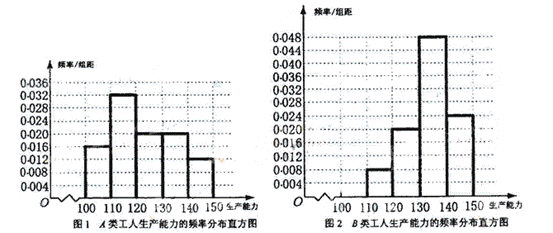 从直方图可以判断:B类工人中个体间的关异程度更小 .
从直方图可以判断:B类工人中个体间的关异程度更小 .
(ii) 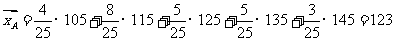 ,
,
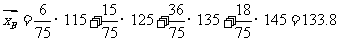 ,
,
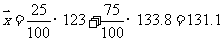
A类工人生产能力的平均数,B类工人生产能力的平均数以及全工厂工人生产能力的平均数的会计值分别为123,133.8和131.1 .
(19)(本小题满分12分)
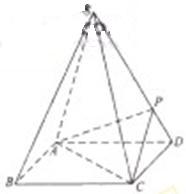 如图,四棱锥S-ABCD 的底面是正方形,每条侧棱的长都是地面边长的
如图,四棱锥S-ABCD 的底面是正方形,每条侧棱的长都是地面边长的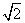 倍,P为侧棱SD上的点。
倍,P为侧棱SD上的点。
(Ⅰ)求证:AC⊥SD;
(Ⅱ)若SD⊥平面PAC,求二面角P-AC-D的大小
(Ⅲ)在(Ⅱ)的条件下,侧棱SC上是否存在一点E,
使得BE∥平面PAC。若存在,求SE:EC的值;
若不存在,试说明理由。
(19)解法一:
(Ⅰ)连BD,设AC交BD于O,由题意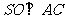 。在正方形ABCD中,
。在正方形ABCD中,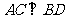 ,所以
,所以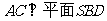 ,得
,得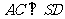 .
.
(Ⅱ)设正方形边长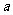 ,则
,则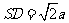 。
。
又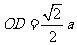 ,所以
,所以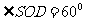 ,
,
连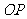 ,由(Ⅰ)知
,由(Ⅰ)知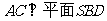 ,所以
,所以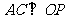 ,
,
且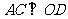 ,所以
,所以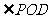 是二面角
是二面角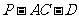 的平面角。
的平面角。
由 ,知
,知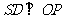 ,所以
,所以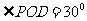 ,
,
即二面角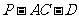 的大小为
的大小为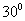 。
。
(Ⅲ)在棱SC上存在一点E,使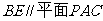
由(Ⅱ)可得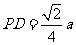 ,故可在
,故可在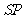 上取一点
上取一点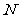 ,使
,使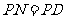 ,过
,过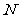 作
作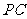 的平行线与
的平行线与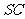 的交点即为
的交点即为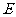 。连BN。在
。连BN。在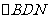 中知
中知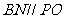 ,又由于
,又由于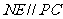 ,故平面
,故平面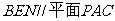 ,得
,得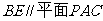 ,由于
,由于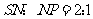 ,故
,故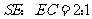 .
.
解法二:
(Ⅰ);连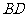 ,设
,设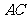 交于
交于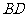 于
于 ,由题意知
,由题意知 .以O为坐标原点,
.以O为坐标原点, 分别为
分别为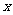 轴、
轴、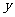 轴、
轴、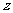 轴正方向,建立坐标系
轴正方向,建立坐标系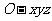 如图。
如图。
设底面边长为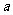 ,则高
,则高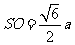 。
。
于是 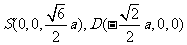
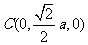


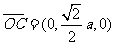

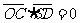
故 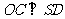
从而 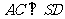
(Ⅱ)由题设知,平面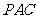 的一个法向量
的一个法向量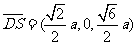 ,平面
,平面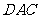 的一个法向量
的一个法向量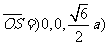 ,设所求二面角为
,设所求二面角为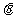 ,则
,则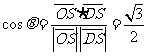 ,所求二面角的大小为
,所求二面角的大小为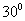
(Ⅲ)在棱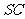 上存在一点
上存在一点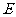 使
使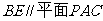 .
.
由(Ⅱ)知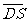 是平面
是平面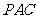 的一个法向量,
的一个法向量,
且 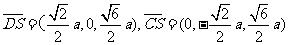
设 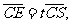
则 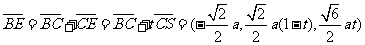
而 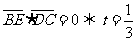
即当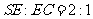 时,
时,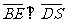


而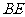 不在平面
不在平面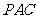 内,故
内,故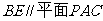
(20)(本小题满分12分)
已知椭圆C的中心为直角坐标系xOy的原点,焦点在s轴上,它的一个顶点到两个焦点的距离分别是7和1.
(Ⅰ)求椭圆C的方程;
(Ⅱ)若P为椭圆C上的动点,M为过P且垂直于x轴的直线上的点,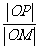 =λ,求点M的轨迹方程,并说明轨迹是什么曲线。
=λ,求点M的轨迹方程,并说明轨迹是什么曲线。
(20)解:
(Ⅰ)设椭圆长半轴长及半焦距分别为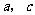 ,由已知得
,由已知得
 ,
,
所以椭圆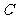 的标准方程为
的标准方程为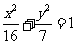


(Ⅱ)设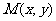 ,其中
,其中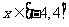 。由已知
。由已知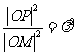 及点
及点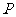 在椭圆
在椭圆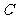 上可得
上可得
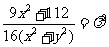 。
。
整理得 ,其中
,其中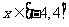 。
。
(i)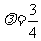 时。化简得
时。化简得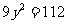
所以点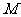 的轨迹方程为
的轨迹方程为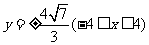 ,轨迹是两条平行于
,轨迹是两条平行于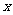 轴的线段。
轴的线段。
(ii)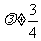 时,方程变形为
时,方程变形为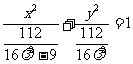 ,其中
,其中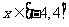
当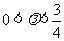 时,点
时,点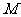 的轨迹为中心在原点、实轴在
的轨迹为中心在原点、实轴在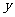 轴上的双曲线满足
轴上的双曲线满足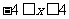 的部分。
的部分。
当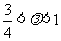 时,点
时,点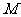 的轨迹为中心在原点、长轴在
的轨迹为中心在原点、长轴在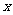 轴上的椭圆满足
轴上的椭圆满足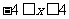 的部分;
的部分;
当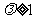 时,点
时,点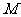 的轨迹为中心在原点、长轴在
的轨迹为中心在原点、长轴在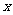 轴上的椭圆;
轴上的椭圆;
(21)(本小题满分12分)
已知函数
(I)
如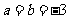 ,求
,求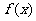 的单调区间;
的单调区间;
(II)
若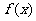 在
在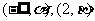 单调增加,在
单调增加,在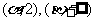 单调减少,证明
单调减少,证明
 <6.
<6.
(21)解:
(Ⅰ)当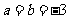 时,
时,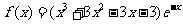 ,故
,故 


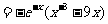
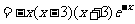
当
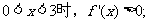
当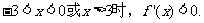
从而 单调减少.
单调减少.
(Ⅱ)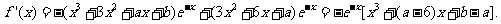
由条件得: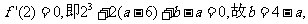 从而
从而
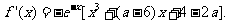
因为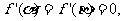 所以
所以
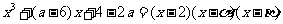
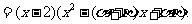
将右边展开,与左边比较系数得,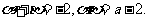 故
故

又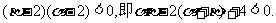 由此可得
由此可得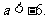
于是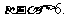
请考生在第(22)、(23)、(24)三题中任选一题作答,如果多做,则按所做的第一题记分。作答时用2B铅笔在答题卡上把所选题目对应的题号涂黑。
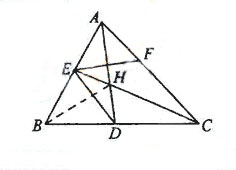
(22)本小题满分10分)选修4-1:几何证明选讲
如图,已知 的两条角平分线
的两条角平分线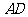 和
和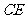 相交于H,
相交于H,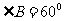 ,F在
,F在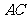 上,
上,
且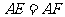 。
。
(I) 证明:B,D,H,E四点共圆:
(II)
证明: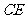 平分
平分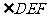 。
。
(22)解:
(Ⅰ)在△ABC中,因为∠B=60°,
所以∠BAC+∠BCA=120°.
因为AD,CE是角平分线,
所以∠HAC+∠HCA=60°,
故∠AHC=120°. 

于是∠EHD=∠AHC=120°.
因为∠EBD+∠EHD=180°,
所以B,D,H,E四点共圆.
(Ⅱ)连结BH,则BH为∠ABC的平分线,得∠HBD=30°
由(Ⅰ)知B,D,H,E四点共圆,
所以∠CED=∠HBD=30°.
又∠AHE=∠EBD=60°,由已知可得EF⊥AD,
可得∠CEF=30°.
所以CE平分∠DEF.
(23)(本小题满分10分)选修4-4:坐标系与参数方程。
已知曲线C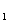 :
: (t为参数), C
(t为参数), C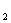 :
: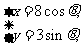 (
(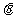 为参数)。
为参数)。
(1)化C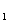 ,C
,C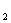 的方程为普通方程,并说明它们分别表示什么曲线;
的方程为普通方程,并说明它们分别表示什么曲线;
(2)若C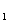 上的点P对应的参数为
上的点P对应的参数为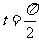 ,Q为C
,Q为C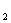 上的动点,求
上的动点,求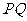 中点
中点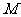 到直线
到直线
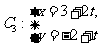 (t为参数)距离的最小值。
(t为参数)距离的最小值。
(23)解:
(Ⅰ)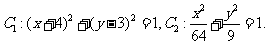
 为圆心是(
为圆心是(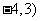 ,半径是1的圆.
,半径是1的圆.
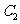 为中心是坐标原点,焦点在x轴上,长半轴长是8,短半轴长是3的椭圆.
为中心是坐标原点,焦点在x轴上,长半轴长是8,短半轴长是3的椭圆.
(Ⅱ)当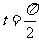 时,
时,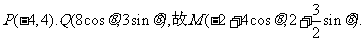
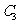 为直线
为直线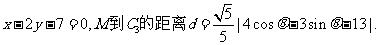
从而当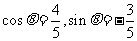 时,
时,
(24)(本小题满分10分)选修4-5:不等式选讲
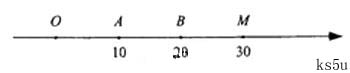
如图,O为数轴的原点,A,B,M为数轴上三点,C为线段OM上的动点,设x表示C与原点的距离,y 表示C到A距离4倍与C道B距离的6倍的和.
(1)将y表示成x的函数;
(2)要使y的值不超过70,x 应该在什么范围内取值?

(24)解:
(Ⅰ)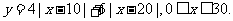
(Ⅱ)依题意,x满足
{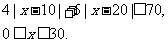
解不等式组,其解集为[9,23]
所以 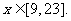 w.w.w.k.s.5.u.c
w.w.w.k.s.5.u.c
(13)设已知抛物线C的顶点在坐标原点,焦点为F(1,0),直线l与抛物线C相交于A,B两点。若AB的中点为(2,2),则直线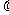 的方程为_____________.
的方程为_____________.
解析:抛物线的方程为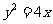 ,
,
答案:y=x
(14)已知函数y=sin(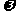 x+
x+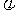 )(
)(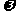 >0, -
>0, -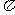

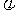 <
<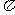 )的图像如图所示,则
)的图像如图所示,则 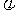 =________________
=________________
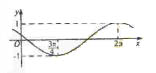 解析:由图可知,
解析:由图可知,
答案: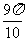
(15)7名志愿者中安排6人在周六、周日两天参加社区公益活动。若每天安排3人,则不同的安排方案共有________________种(用数字作答)。
解析: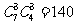 ,答案:140
,答案:140
(16)等差数列{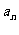 }前n项和为
}前n项和为 。已知
。已知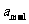 +
+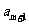 -
-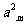 =0,
=0,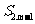 =38,则m=_______
=38,则m=_______
解析:由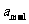 +
+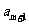 -
-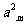 =0得到
=0得到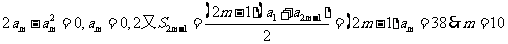 。
。
答案10
(17)(本小题满分12分) 

如图,为了解某海域海底构造,在海平面内一条直线上的A,B,C三点进行测量,已知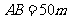 ,
,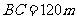 ,于A处测得水深
,于A处测得水深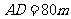 ,于B处测得水深
,于B处测得水深 ,于C处测得水深
,于C处测得水深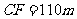 ,求∠DEF的余弦值。
,求∠DEF的余弦值。


(18)(本小题满分12分)
如图,在三棱锥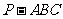 中,⊿
中,⊿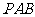 是等边三角形,∠PAC=∠PBC=90 º
是等边三角形,∠PAC=∠PBC=90 º
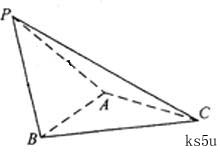 (Ⅰ)证明:AB⊥PC
(Ⅰ)证明:AB⊥PC
(Ⅱ)若 ,且平面
,且平面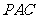 ⊥平面
⊥平面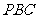 ,
,
求三棱锥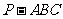 体积。
体积。
(19)(本小题满分12分)
某工厂有工人1000名,其中250名工人参加过短期培训(称为A类工人),另外750名工人参加过长期培训(称为B类工人).现用分层抽样方法(按A类,B类分二层)从该工厂的工人中共抽查100名工人,调查他们的生产能力(生产能力指一天加工的零件数).
(Ⅰ)A类工人中和B类工人各抽查多少工人?
(Ⅱ)从A类工人中抽查结果和从B类工人中的抽查结果分别如下表1和表2
表1:
|
生产能力分组 |
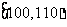 |
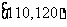 |
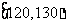 |
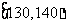 |
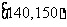 |
|
人数 |
4 |
8 |
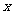 |
5 |
3 |
表2:
|
生产能力分组 |
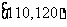 |
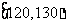 |
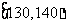 |
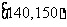 |
|
人数 |
6 |
y |
36 |
18 |
(1) 先确定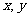 ,再在答题纸上完成下列频率分布直方图。就生产能力而言,A类工人中个体间的差异程度与B类工人中个体间的差异程度哪个更小?(不用计算,可通过观察直方图直接回答结论)
,再在答题纸上完成下列频率分布直方图。就生产能力而言,A类工人中个体间的差异程度与B类工人中个体间的差异程度哪个更小?(不用计算,可通过观察直方图直接回答结论)
(ii)分别估计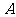 类工人和
类工人和 类工人生产能力的平均数,并估计该工厂工人和生产能力的平均数(同一组中的数据用该区间的中点值作代表)。
类工人生产能力的平均数,并估计该工厂工人和生产能力的平均数(同一组中的数据用该区间的中点值作代表)。
(20)(本小题满分12分)
已知椭圆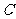 的中心为直角坐标系
的中心为直角坐标系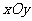 的原点,焦点在
的原点,焦点在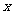 轴上,它的一个项点到两个
轴上,它的一个项点到两个
焦点的距离分别是7和1
(I)
求椭圆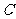 的方程‘
的方程‘
(II)
若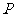 为椭圆
为椭圆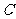 的动点,
的动点,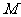 为过
为过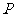 且垂直于
且垂直于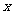 轴的直线上的点,
轴的直线上的点,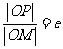
(e为椭圆C的离心率),求点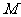 的轨迹方程,并说明轨迹是什么曲线。
的轨迹方程,并说明轨迹是什么曲线。
(21)(本小题满分12分)
已知函数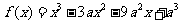 .
.
(1)
设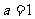 ,求函数
,求函数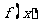 的极值;
的极值;
(2)
若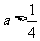 ,且当
,且当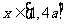 时,
时,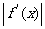
 12a恒成立,试确定
12a恒成立,试确定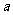 的取值范围.
的取值范围.
请考生在第(22)、(23)、(24)三题中任选一题作答,如果多做,则按所做的第一题计分。作答时用2B铅笔在答题卡上把所选题目对应的题号涂黑。 

(22)(本小题满分10分)选修4-1;几何证明选讲
 如图,已知
如图,已知 ABC中的两条角平分线
ABC中的两条角平分线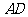 和
和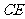 相交于
相交于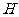 ,
, B=60
B=60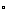 ,
,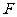 在
在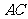 上,且
上,且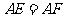 。
。 

(1)证明: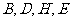 四点共圆;
四点共圆;
(2)证明:CE平分 DEF。
DEF。
(23)(本小题满分10分)选修4-4:坐标系与参数方程。
已知曲线C :
: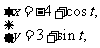 (t为参数), C
(t为参数), C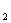 :
: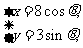 (
(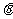 为参数)。
为参数)。
(1)化C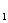 ,C
,C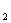 的方程为普通方程,并说明它们分别表示什么曲线;
的方程为普通方程,并说明它们分别表示什么曲线;
(2)若C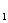 上的点P对应的参数为
上的点P对应的参数为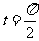 ,Q为C
,Q为C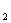 上的动点,求
上的动点,求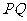 中点
中点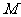 到直线
到直线
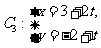 (t为参数)距离的最小值。
(t为参数)距离的最小值。 

(24)(本小题满分10分)选修4-5:不等式选讲
如图, 为数轴的原点,
为数轴的原点, 为数轴上三点,
为数轴上三点, 为线段
为线段 上的动点,设
上的动点,设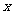 表示
表示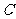 与原点的距离,
与原点的距离,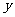 表示
表示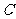 到
到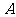 距离4倍与
距离4倍与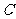 到
到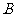 距离的6倍的和.
距离的6倍的和.
(1)将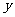 表示为
表示为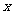 的函数;
的函数;
(2)要使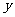 的值不超过70,
的值不超过70,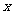 应该在什么范围内取值?
应该在什么范围内取值?


2009年普通高等学校招生全国统一考试
(17)(本小题满分12分)
在△ABC中,A、B为锐角,角A、B、C所对的边分别为a、b、c,且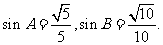
(Ⅰ)求A+B的值;
(Ⅱ)若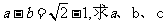 得值.
得值. 

(18)(本小题满分12分)
为振兴旅游业,四川省2009年面向国内发行总量为2000万张的熊猫优惠卡,向省外人士发行的是熊猫金卡(简称金卡),向省内人士发行的是熊猫银卡(简称银卡),某旅游公司组织了一个有36名游客的旅游团到四川名胜旅游,其中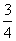 是省外游客,其余是省内游客,在省外游客中有
是省外游客,其余是省内游客,在省外游客中有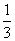 持金卡,在省内游客中有
持金卡,在省内游客中有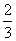 持银卡.
持银卡.
(Ⅰ)在该团中随即采访2名游客,求恰有1人持银卡的概率; 

(Ⅱ)在该团中随机采访2名游客,求其中持金卡与持银卡人数相当的概率.
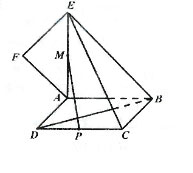 (19)(本小题满分12分)如图,正方形ABCD所在平面与平面四边形ABEF所在平面互相垂直,△ABE是等腰直角三角形,AB=AE,FA=FE,∠AEF=45°.
(19)(本小题满分12分)如图,正方形ABCD所在平面与平面四边形ABEF所在平面互相垂直,△ABE是等腰直角三角形,AB=AE,FA=FE,∠AEF=45°.


(Ⅰ)求证:EF⊥平面BCE;
(Ⅱ)设线段CD、AE的中点分别为P、M,求证:PM∥平面BCE;
(Ⅲ)求二面角F-BD-A的大小.
(20)(本小题满分12分)
已知函数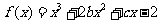 的图象在与x轴交点处的切线方程是
的图象在与x轴交点处的切线方程是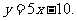
(Ⅰ)求函数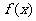 的解析式;
的解析式; 

(Ⅱ)设函数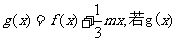 的极值存在,求实数m的取值范围以及函数
的极值存在,求实数m的取值范围以及函数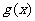 取得极值时对应的自变量x的值.
取得极值时对应的自变量x的值.


(21)(本小题满分12分)
已知椭圆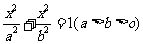 的左、右焦点分别为
的左、右焦点分别为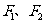 ,离心率
,离心率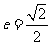 ,右准线方程为x=2.
,右准线方程为x=2. 

(Ⅰ)求椭圆的标准方程;
(Ⅱ)过点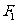 的直线
的直线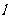 与该椭圆相交于M、N两点,且
与该椭圆相交于M、N两点,且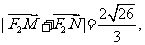 求直线
求直线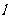 的方程式.
的方程式. 

(22)(本小题满分14分)
设数列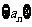 的前n项和为
的前n项和为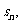 对任意的正整数n,都有
对任意的正整数n,都有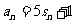 成立,记
成立,记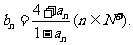


(Ⅰ)求数列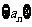 与数列
与数列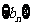 的通项公式;
的通项公式;
(Ⅱ)设数列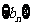 的前n项和为R
的前n项和为R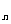 ,是否存在正整数k,使得
,是否存在正整数k,使得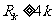 成立?若存在,找出一个正整数k;若不存在,请说明理由;
成立?若存在,找出一个正整数k;若不存在,请说明理由;
(Ⅲ)记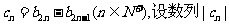 的前n项和味
的前n项和味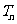 ,求证:对任意正整数n,都有
,求证:对任意正整数n,都有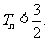
 (13)抛物线
(13)抛物线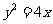 的焦点到准线的距离是
.
的焦点到准线的距离是
.
(14)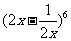 的展开式的常数项是
.(用数字作答)
的展开式的常数项是
.(用数字作答)
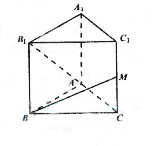
(15)如图,已知正三棱柱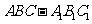 的各条棱长都相等,M是侧棱
的各条棱长都相等,M是侧棱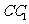 的中点,侧异面直线
的中点,侧异面直线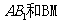 所成的角的大小是
.
所成的角的大小是
.
(16)设V是已知平面M上所有向量的集合,对于映射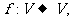
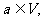 记
记
 若映射
若映射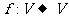 满足:对所有
满足:对所有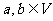 及任意实数
及任意实数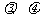 都有
都有 

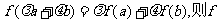 称为平面M上的线性变换,现有下列命题:
称为平面M上的线性变换,现有下列命题:
① 设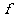 是平面M上的线性变换,
是平面M上的线性变换,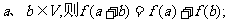
② 若e是平面M上的单位向量,对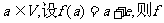 是平面M上的线性变换;
是平面M上的线性变换;
③ 对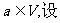
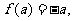 则
则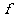 是平面M上的线性变换;
是平面M上的线性变换;
④ 设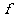 是平面M上的线性变换,
是平面M上的线性变换,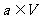 ,则对任意实数k均有
,则对任意实数k均有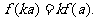
其中的真命题是
.(写出所有真命题的编号) 

17(本小题满分10分)
设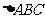 的内角
的内角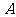 、
、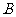 、
、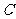 的对边长分别为
的对边长分别为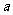 、
、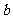 、
、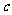 ,
,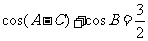 ,
,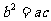 ,求
,求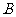 。
。
分析:由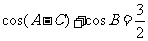 ,易想到先将
,易想到先将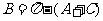 代入
代入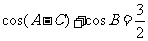 得
得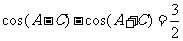 。然后利用两角和与差的余弦公式展开得
。然后利用两角和与差的余弦公式展开得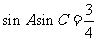 ;又由
;又由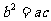 ,利用正弦定理进行边角互化,得
,利用正弦定理进行边角互化,得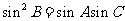 ,进而得
,进而得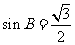 .故
.故 。大部分考生做到这里忽略了检验,事实上,当
。大部分考生做到这里忽略了检验,事实上,当 时,由
时,由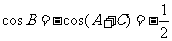 ,进而得
,进而得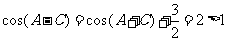 ,矛盾,应舍去。
,矛盾,应舍去。
也可利用若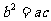 则
则 从而舍去
从而舍去 。不过这种方法学生不易想到。
。不过这种方法学生不易想到。
 评析:本小题考生得分易,但得满分难。
评析:本小题考生得分易,但得满分难。
18(本小题满分12分)
如图,直三棱柱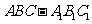 中,
中, 、
、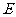 分别为
分别为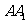 、
、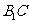 的中点,
的中点,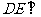 平面
平面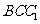
(I)证明: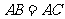
(II)设二面角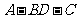 为60°,求
为60°,求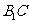 与平面
与平面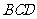 所成的角的大小。
所成的角的大小。
(I)分析一:连结BE,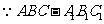 为直三棱柱,
为直三棱柱, 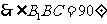
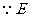 为
为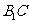 的中点,
的中点,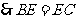 。又
。又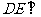 平面
平面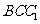 ,
,
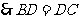 (射影相等的两条斜线段相等)而
(射影相等的两条斜线段相等)而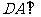 平面
平面 ,
,
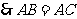 (相等的斜线段的射影相等)。
(相等的斜线段的射影相等)。
分析二:取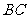 的中点
的中点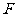 ,证四边形
,证四边形 为平行四边形,进而证
为平行四边形,进而证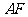 ∥
∥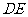 ,
, ,得
,得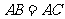 也可。
也可。
分析三:利用空间向量的方法。具体解法略。
(II)分析一:求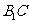 与平面
与平面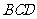 所成的线面角,只需求点
所成的线面角,只需求点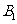 到面
到面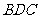 的距离即可。
的距离即可。
 作
作 于
于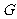 ,连
,连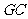 ,则
,则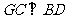 ,
,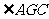 为二面角
为二面角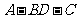 的平面角,
的平面角,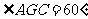 .不妨设
.不妨设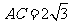 ,则
,则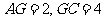 .在
.在 中,由
中,由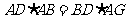 ,易得
,易得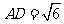 .
.
设点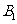 到面
到面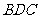 的距离为
的距离为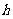 ,
,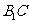 与平面
与平面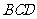 所成的角为
所成的角为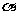 。利用
。利用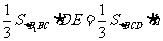 ,可求得
,可求得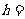
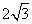 ,又可求得
,又可求得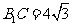
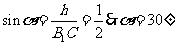
即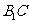 与平面
与平面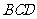 所成的角为
所成的角为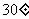
分析二:作出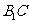 与平面
与平面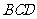 所成的角再行求解。如图可证得
所成的角再行求解。如图可证得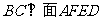 ,所以面
,所以面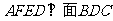 。由分析一易知:四边形
。由分析一易知:四边形 为正方形,连
为正方形,连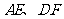 ,并设交点为
,并设交点为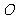 ,则
,则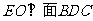 ,
,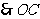 为
为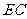 在面
在面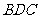 内的射影。
内的射影。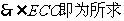 。以下略。
。以下略。
分析三:利用空间向量的方法求出面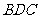 的法向量
的法向量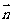 ,则
,则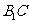 与平面
与平面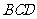 所成的角即为
所成的角即为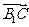 与法向量
与法向量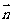 的夹角的余角。具体解法详见高考试题参考答案。
的夹角的余角。具体解法详见高考试题参考答案。
总之在目前,立体几何中的两种主要的处理方法:传统方法与向量的方法仍处于各自半壁江山的状况。命题人在这里一定会兼顾双方的利益。
19(本小题满分12分)
设数列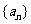 的前
的前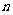 项和为
项和为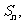 已知
已知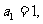
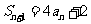
(I)设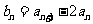 ,证明数列
,证明数列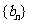 是等比数列
是等比数列
(II)求数列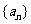 的通项公式。
的通项公式。
解:(I)由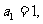 及
及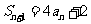 ,有
,有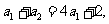
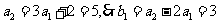
由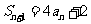 ,...① 则当
,...① 则当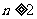 时,有
时,有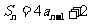 .....②
.....②
②-①得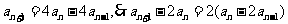
又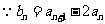 ,
,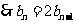
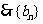 是首项
是首项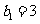 ,公比为2的等比数列.
,公比为2的等比数列.
(II)由(I)可得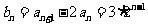 ,
,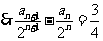
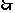 数列
数列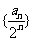 是首项为
是首项为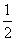 ,公差为
,公差为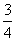 的等比数列.
的等比数列.
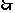
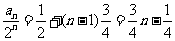 ,
,
评析:第(I)问思路明确,只需利用已知条件寻找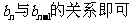 .
.
第(II)问中由(I)易得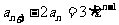 ,这个递推式明显是一个构造新数列的模型:
,这个递推式明显是一个构造新数列的模型: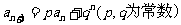 ,主要的处理手段是两边除以
,主要的处理手段是两边除以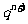 .
.
总体来说,09年高考理科数学全国I、Ⅱ这两套试题都将数列题前置,主要考查构造新数列(全国I还考查了利用错位相减法求前n项和的方法),一改往年的将数列结合不等式放缩法问题作为押轴题的命题模式。具有让考生和一线教师重视教材和基础知识、基本方法基本技能,重视两纲的导向作用。也可看出命题人在有意识降低难度和求变的良苦用心。
20(本小题满分12分)
某车间甲组有10名工人,其中有4名女工人;乙组有5名工人,其中有3名女工人,现采用分层抽样方法(层内采用不放回简单随机抽样)从甲、乙两组中共抽取3名工人进行技术考核。
(I)求从甲、乙两组各抽取的人数;
(II)求从甲组抽取的工人中恰有1名女工人的概率;
(III)记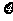 表示抽取的3名工人中男工人数,求
表示抽取的3名工人中男工人数,求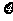 的分布列及数学期望。
的分布列及数学期望。 

分析:(I)这一问较简单,关键是把握题意,理解分层抽样的原理即可。另外要注意此分层抽样与性别无关。
(II)在第一问的基础上,这一问处理起来也并不困难。
从甲组抽取的工人中恰有1名女工人的概率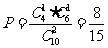
(III)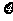 的可能取值为0,1,2,3
的可能取值为0,1,2,3
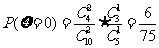 ,
,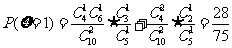 ,
,
 ,
,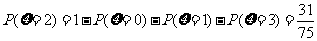
分布列及期望略。
评析:本题较常规,比08年的概率统计题要容易。在计算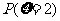 时,采用分类的方法,用直接法也可,但较繁琐,考生应增强灵活变通的能力。
时,采用分类的方法,用直接法也可,但较繁琐,考生应增强灵活变通的能力。
(21)(本小题满分12分)
已知椭圆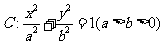 的离心率为
的离心率为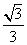 ,过右焦点F的直线
,过右焦点F的直线 与
与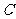 相交于
相交于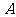 、
、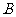 两点,当
两点,当 的斜率为1时,坐标原点
的斜率为1时,坐标原点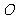 到
到 的距离为
的距离为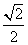
(I)求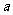 ,
,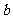 的值;
的值;
(II)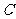 上是否存在点P,使得当
上是否存在点P,使得当 绕F转到某一位置时,有
绕F转到某一位置时,有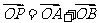 成立?
成立?
若存在,求出所有的P的坐标与 的方程;若不存在,说明理由。
的方程;若不存在,说明理由。
解:(I)设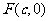 ,直线
,直线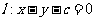 ,由坐标原点
,由坐标原点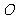 到
到 的距离为
的距离为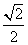
则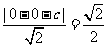 ,解得
,解得 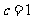 .又
.又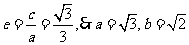 .
.
(II)由(I)知椭圆的方程为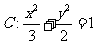 .设
.设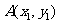 、
、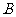
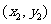
由题意知 的斜率为一定不为0,故不妨设
的斜率为一定不为0,故不妨设 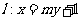
代入椭圆的方程中整理得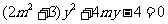 ,显然
,显然 。
。
由韦达定理有: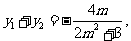
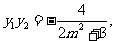 ........①
........①
.假设存在点P,使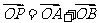 成立,则其充要条件为:
成立,则其充要条件为:
点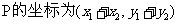 ,点P在椭圆上,即
,点P在椭圆上,即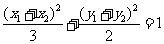 。
。
整理得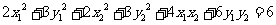 。
。 

又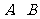 在椭圆上,即
在椭圆上,即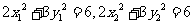 .
.
故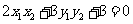 ................................②
................................②
将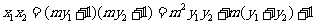 及①代入②解得
及①代入②解得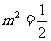
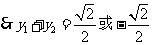 ,
,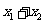 =
=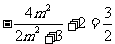 ,即
,即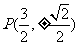 .
.
当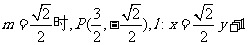 ;
;
当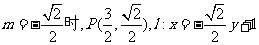 .
.
评析:处理解析几何题,学生主要是在“算”上的功夫不够。所谓“算”,主要讲的是算理和算法。算法是解决问题采用的计算的方法,而算理是采用这种算法的依据和原因,一个是表,一个是里,一个是现象,一个是本质。有时候算理和算法并不是截然区分的。例如:三角形的面积是用底乘高的一半还是用两边与夹角的正弦的一半,还是分割成几部分来算?在具体处理的时候,要根据具体问题及题意边做边调整,寻找合适的突破口和切入点。
22.(本小题满分12分)
设函数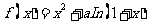 有两个极值点
有两个极值点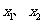 ,且
,且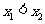
(I)求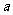 的取值范围,并讨论
的取值范围,并讨论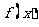 的单调性;
的单调性;
(II)证明: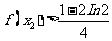
解: (I)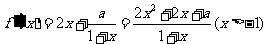
令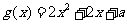 ,其对称轴为
,其对称轴为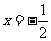 。由题意知
。由题意知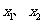 是方程
是方程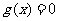 的两个均大于
的两个均大于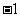 的不相等的实根,其充要条件为
的不相等的实根,其充要条件为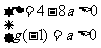 ,得
,得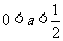
⑴当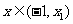 时,
时,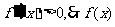 在
在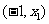 内为增函数;
内为增函数;
⑵当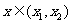 时,
时,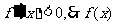 在
在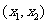 内为减函数;
内为减函数;
⑶当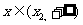 时,
时,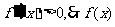 在
在 内为增函数;
内为增函数;
(II)由(I)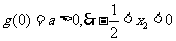 ,
,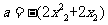
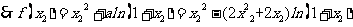
设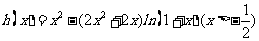 ,
,
则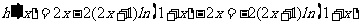
⑴当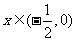 时,
时,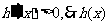 在
在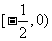 单调递增;
单调递增;
⑵当 时,
时,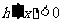 ,
,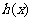 在
在 单调递减。
单调递减。
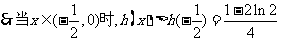
故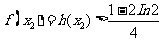 .
. 

16. 已知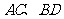 为圆
为圆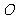 :
: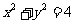 的两条相互垂直的弦,垂足为
的两条相互垂直的弦,垂足为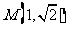 ,则四边形
,则四边形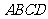 的面积的最大值为
。
的面积的最大值为
。
解:设圆心 到
到 的距离分别为
的距离分别为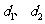 ,则
,则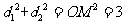 .
.
四边形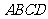 的面积
的面积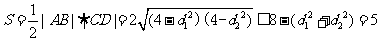
15.设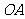 是球
是球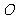 的半径,
的半径,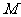 是
是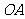 的中点,过
的中点,过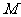 且与
且与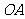 成45°角的平面截球
成45°角的平面截球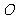 的表面得到圆
的表面得到圆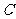 。若圆
。若圆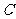 的面积等于
的面积等于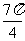 ,则球
,则球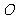 的表面积等于
的表面积等于 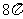 .
.
解:设球半径为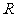 ,圆
,圆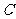 的半径为
的半径为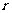 ,
,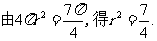
因为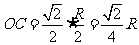 。由
。由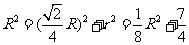 得
得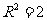 .故球
.故球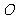 的表面积等于
的表面积等于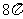 .
.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com