
3.要正确理解和灵活运用参数a,b,c,,e的几何意义与相互关系;
2.求椭圆方程,常用待定系数法,定义法,首先确定曲线类型和方程的形式,再由题设条件确定参数值,应“特别”掌握;
(1)当焦点位置不确定时,方程可能有两种形式,应防止遗漏;
(2)两种标准方程中,总有a>b>0,c2=a2-b2并且椭圆的焦点总在长轴上;
1.椭圆定义是解决问题的出发点,一般地,涉及a、b、c的问题先考虑第一定义,涉及e、d及焦半径的问题行急需处理 虑第二定义;
[例1]若椭圆ax2+by2=1与直线x+y=1交于A、B两点,M为AB的中点,直线OM(O为原点)的斜率为 ,且OA⊥OB,求椭圆的方程.
,且OA⊥OB,求椭圆的方程.
分析:欲求椭圆方程,需求a、b,为此需要得到关于a、b的两个方程,由OM的斜率为 .OA⊥OB,易得a、b的两个方程.
.OA⊥OB,易得a、b的两个方程.
解法1:设A(x1,y1),B(x2,y2),M(x0,y0).
|
|
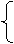 x+y=1,
x+y=1,
ax2+by2=1,
∴x0= =
= ,y0=
,y0= =1-
=1- =
=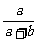 .
.
∴M( ,
,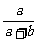 ).
).
∵kOM= ,∴b=
,∴b= a. ①
a. ①
∵OA⊥OB,∴ ·
· =-1.
=-1.
∴x1x2+y1y2=0.
∵x1x2= ,y1y2=(1-x1)(1-x2),
,y1y2=(1-x1)(1-x2),
∴y1y2=1-(x1+x2)+x1x2
=1- +
+ =
= .
.
∴ +
+ =0.
=0.
∴a+b=2. ②
由①②得a=2( -1),b=2
-1),b=2 (
( -1).
-1).
∴所求方程为2( -1)x2+2
-1)x2+2 (
( -1)y2=1.
-1)y2=1.
法2:(点差法)由ax1+by1=1, ax2+by2=1相减得
 ,即
,即 …下同法1.
…下同法1.
提炼方法:1.设而不求,即设出A(x1,y1),B(x2,y2),借助韦达定理推出b= a..再由OA⊥OB得x1x2+y1y2=0,转换出a,b的又一关系式,
a..再由OA⊥OB得x1x2+y1y2=0,转换出a,b的又一关系式,
2.点差法得b= a.…
a.…
[例2](2005湖南) 已知椭圆C: +
+ =1(a>b>0)的左.右焦点为F1、F2,离心率为e. 直线,l:y=ex+a与x轴.y轴分别交于点A、B,M是直线l与椭圆C的一个公共点,P是点F1关于直线l的对称点,设
=1(a>b>0)的左.右焦点为F1、F2,离心率为e. 直线,l:y=ex+a与x轴.y轴分别交于点A、B,M是直线l与椭圆C的一个公共点,P是点F1关于直线l的对称点,设 =λ
=λ .
.
(Ⅰ)证明:λ=1-e2;
(Ⅱ)若 ,△MF1F2的周长为6;写出椭圆C的方程;(理科无此问)
,△MF1F2的周长为6;写出椭圆C的方程;(理科无此问)
(Ⅲ)确定λ的值,使得△PF1F2是等腰三角形.
(Ⅰ)证法一:因为A、B分别是直线l: 与x轴、y轴的交点,所以A、B的坐标分别是
与x轴、y轴的交点,所以A、B的坐标分别是 .
.
所以点M的坐标是( ). 由
). 由
即 .
.
证法二:因为A、B分别是直线l: 与x轴、y轴的交点,所以A、B的坐标分别是
与x轴、y轴的交点,所以A、B的坐标分别是 设M的坐标是
设M的坐标是
所以 因为点M在椭圆上,所以
因为点M在椭圆上,所以 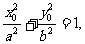
即
 解得
解得
(Ⅱ)当 时,
时, ,所以
,所以 由△MF1F2的周长为6,得
由△MF1F2的周长为6,得
所以 椭圆方程为
椭圆方程为
(Ⅲ)解法一:因为PF1⊥l,所以∠PF1F2=90°+∠BAF1为钝角,要使△PF1F2为等腰三角形,必有|PF1|=|F1F2|,即
设点F1到l的距离为d,由
得 所以
所以
即当 △PF1F2为等腰三角形.
△PF1F2为等腰三角形.
解法二:因为PF1⊥l,所以∠PF1F2=90°+∠BAF1为钝角,要使△PF1F2为等腰三角形,必有|PF1|=|F1F2|,
设点P的坐标是 ,
,
则
由|PF1|=|F1F2|得
两边同时除以4a2,化简得 从而
从而
于是 . 即当
. 即当 时,△PF1F2为等腰三角形.
时,△PF1F2为等腰三角形.
[例3](2005春上海)(1)求右焦点坐标是 ,且经过点
,且经过点 的椭圆的标准方程;
的椭圆的标准方程;
(2)已知椭圆 的方程是
的方程是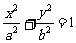
 . 设斜率为
. 设斜率为 的直线
的直线 ,交椭圆
,交椭圆 于
于
 两点,
两点, 的中点为
的中点为 . 证明:当直线
. 证明:当直线 平行移动时,动点
平行移动时,动点 在一条过原点的定直线上;
在一条过原点的定直线上;
(3)利用(2)所揭示的椭圆几何性质,用作图方法找出下面给定椭圆的中心,简要写出作图步骤,并在图中标出椭圆的中心.


解:(1)设椭圆的标准方程为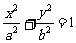 ,
, ,
,
∴  ,即椭圆的方程为
,即椭圆的方程为 ,
,
∵ 点( )在椭圆上,∴
)在椭圆上,∴  ,
,
解得  或
或 (舍),
(舍),
由此得 ,即椭圆的标准方程为
,即椭圆的标准方程为 .
.
(2)设直线 的方程为
的方程为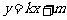 ,
,
与椭圆 的交点
的交点 (
( )、
)、 (
( ),
),
则有 ,
,
解得  ,
,
∵  ,∴
,∴  ,即
,即  .
.
则 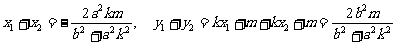 ,
,
∴  中点
中点 的坐标为
的坐标为 .
.
∴ 线段 的中点
的中点 在过原点的直线
在过原点的直线  上.
上.
(3)如图,作两条平行直线分别交椭圆于 、
、 和
和 ,并分别取
,并分别取 、
、 的中点
的中点 ,连接直线
,连接直线 ;又作两条平行直线(与前两条直线不平行)分别交椭圆于
;又作两条平行直线(与前两条直线不平行)分别交椭圆于 、
、 和
和 ,并分别取
,并分别取 、
、 的中点
的中点 ,连接直线
,连接直线 ,那么直线
,那么直线 和
和 的交点
的交点 即为椭圆中心.
即为椭圆中心.


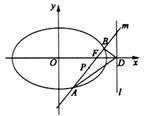
[例4] (2006江西)如图,椭圆 的右焦点为
的右焦点为 ,过点
,过点 的一动直线
的一动直线 绕点
绕点 转动,并且交椭圆于
转动,并且交椭圆于 、
、 两点,
两点,  为线段
为线段 的中点.
的中点.
(1)
求点 的轨迹
的轨迹 的方程;
的方程;
(2)
若在 的方程中,令
的方程中,令 确定
确定 的值,使原点距椭圆
的值,使原点距椭圆 的右准线
的右准线 最远.此时设
最远.此时设 与
与 轴交点为
轴交点为 ,当直线
,当直线 绕点
绕点 转动到什么位置时,三角形
转动到什么位置时,三角形 的面积最大?
的面积最大?
解:如图
(1)设椭圆 上的点
上的点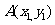 、
、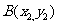 ,又设
,又设 点坐标为
点坐标为 ,则
,则
|
 ………………①
………………①
 当
当 不垂直
不垂直 轴时,
轴时,
由①-②得

 当
当  垂直于
垂直于 轴时,点
轴时,点 即为点
即为点 ,满足方程(*).
,满足方程(*).
故所求点 的轨迹
的轨迹 的方程为:
的方程为:  .
.
(2)因为,椭圆 右准线
右准线 方程是
方程是 ,原点距椭圆
,原点距椭圆 的右准线
的右准线 的距离为
的距离为 ,
,

 时,上式达到最大值,所以当
时,上式达到最大值,所以当 时,原点距椭圆
时,原点距椭圆 的右准线
的右准线 最远.
最远.
此时 .
.
设椭圆  上的点
上的点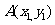 、
、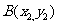 ,
,
△ 的面积
的面积
设直线 的方程为
的方程为 ,代入
,代入 中,得
中,得
由韦达定理得

令 ,得
,得 ,当
,当 取等号.
取等号.
因此,当直线 绕点
绕点 转动到垂直
转动到垂直 轴位置时, 三角形
轴位置时, 三角形 的面积最大.
的面积最大.
特别提醒:注意这种直线方程的设法,适用于 “含斜率不存在,而无斜率为零的情况”.
[研讨.欣赏](1)已知点P的坐标是(-1,-3),F是椭圆 的右焦点,点Q在椭圆上移动,当
的右焦点,点Q在椭圆上移动,当 取最小值时,求点Q的坐标,并求出其最小值。
取最小值时,求点Q的坐标,并求出其最小值。
(2)设椭圆的中心是坐标原点,长轴在x轴上,离心率为 ,已知点P
,已知点P 到这个椭圆上的点的最远距离是
到这个椭圆上的点的最远距离是 ,求这个椭圆的方程,并求椭圆上到点P的距离是
,求这个椭圆的方程,并求椭圆上到点P的距离是 的点的坐标。
的点的坐标。


解(1)由椭圆方程可知a=4,b= ,则c=2,
,则c=2,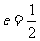 ,
,
椭圆的右准线方程为x=8 过点Q作QQ’ 于点Q’,
于点Q’,
过点P作PP’ 于点P’,则据椭圆的第二定义知,
于点P’,则据椭圆的第二定义知,
 ,
,
易知当P、Q、Q’在同一条线上时,即当Q’与P’点重合时, 才能取得最小值,最小值为8-(-1)=9,此时点Q的纵坐标为-3,代入椭圆方程得
才能取得最小值,最小值为8-(-1)=9,此时点Q的纵坐标为-3,代入椭圆方程得 。
。
因此,当Q点运动到(2,-3)处时,  取最小值9.
取最小值9.
(2)设所求的椭圆的直角坐标方程是 .
.
由 ,解得
,解得 ,设椭圆上的点(x,y)到点P的距离为d.
,设椭圆上的点(x,y)到点P的距离为d.
则
其中 ,如果
,如果 , 则当y=-b时,d2取得最大值
, 则当y=-b时,d2取得最大值
解得b= 与
与 矛盾, 故必有
矛盾, 故必有 当
当 时d2取得最大值,
时d2取得最大值,  解得b=1,a=2 所求椭圆方程为
解得b=1,a=2 所求椭圆方程为 .
.
由 可得椭圆上到点P的距离等于
可得椭圆上到点P的距离等于 的点为
的点为 ,
, .
.
6.根据椭圆的对称性知, ,同理其余两对的和也是
,同理其余两对的和也是 ,
,
又 ,∴
,∴ 
 =35
=35
5.  +
+ =1或
=1或 +
+ =1;
=1;
4.易知圆F2的半径为c,(2a-c)2+c2=4c2,( )2+2(
)2+2( )-2=0,
)-2=0, =
= -1.
-1.
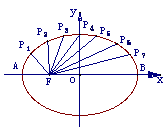
6.(2006四川15)如图把椭圆 的长轴AB分成8份,过每个分点作x轴的垂线交椭圆的上半部分于
的长轴AB分成8份,过每个分点作x轴的垂线交椭圆的上半部分于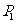 ,
, ,……
,…… 七个点,F是椭圆的一个焦点,则
七个点,F是椭圆的一个焦点,则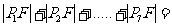 ____________.
____________.
简答提示:1-4.CBBA;
5.椭圆对称轴在坐标轴上,短轴的一个端点与两个焦点构成一个正三角形,焦点到椭圆上的点的最短距离是 ,则这个椭圆方程为__________________.
,则这个椭圆方程为__________________.
4.设F1、F2为椭圆的两个焦点,以F2为圆心作圆F2,已知圆F2经过椭圆的中心,且与椭圆相交于M点,若直线MF1恰与圆F2相切,则该椭圆的离心率e为 ( )
A.  -1
B.2-
-1
B.2- C.
C. D.
D.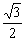
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com