
4、 刘姝威 中央财经大学研究员 颁奖辞:她用自己的大智大勇向一个虚假的神话提出质疑,面对一个强大的集团,面对一张深不可测的网,面对死亡的威胁,她以自己个人的力量坚持着这场强弱悬殊的战争,坚守着正义和良心的壁垒。正是这种中国知识分子的风骨,完美地证明了中国还有一双揉不进沙子的眼睛,推动了中国股市早日走上正轨,推动了中国经济的发展。
3、 王选 中国受害者诉讼原告团团长 颁奖辞:她用柔弱的肩头担负起历史的使命,她用正义的利剑戳穿弥天的谎言,她用坚毅和执著还原历史的真相。她奔走在一条看不见尽头的诉讼之路上,和她相伴的是一群满身历史创伤的老人。她不仅仅是在为日本细菌战中的中国受害者讨还公道,更是为整个人类赖以生存的大规则寻求支撑的力量,告诉世界该如何面对伤害,面对耻辱,面对谎言,面对罪恶,为人类如何继承和延续历史提供了注解。
2、张荣锁 河南辉县上八里镇回龙村党支书 颁奖辞:他已经拥有了财富,但他心里装着还在贫苦生活中的乡亲,他已经走出了大山,但他还想让所有乡亲都能够走出与世隔绝的山崖,他成就了一个多少代人未能实现的梦想,他拿出愚公移山的执著和勇气劈开了大山,在悬崖峭壁上为乡亲们开凿出通往外面世界的大道,更在人们的心中打开了一扇希望之门。它结束了一段贫困的历史,开创出一种崭新的生活。
1、郑培民 湖南省委原副书记
颁奖辞:他身居高位而心系百姓,他以“做官先做人,万事民为先”为自己的行为标准,直到生命的最后时刻仍然不忘自己曾经许下的诺言。他树立了一个共产党人的品德风范,他在人民心里树立起一座公正廉洁为民服务的丰碑。
10.已知数列{an}、{bn}都是由正数组成的等比数列,公比分别为p、q,其中p>q且p≠1,q≠1,设cn=an+bn,Sn为数列{cn}的前n项和,求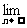
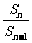 .
.
解:Sn=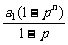 +
+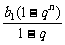 ,
,
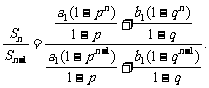
当p>1时,p>q>0,得0<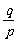 <1,上式分子、分母同除以pn-1,得
<1,上式分子、分母同除以pn-1,得
∴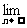
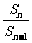 =p.
=p.
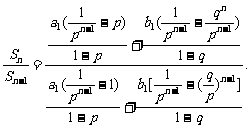
当p<1时,0<q<p<1,
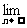
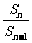 =
=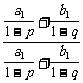 =1.
=1.
[探索题]已知公比为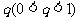 的无穷等比数列
的无穷等比数列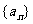 各项的和为9,无穷等比数列
各项的和为9,无穷等比数列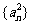 各项的和为
各项的和为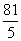
(Ⅰ)求数列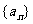 的首项
的首项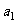 和公比
和公比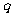 ;
;
(Ⅱ)对给定的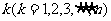 ,设
,设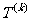 是首项为
是首项为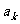 ,公差为
,公差为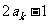 的等差数列.求数列
的等差数列.求数列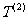 的前10项之和;
的前10项之和;
(Ⅲ)设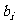 为数列
为数列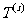 的第
的第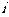 项,
项,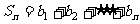 ,求
,求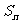 ,并求正整数
,并求正整数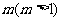 ,使得
,使得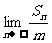 存在且不等于零
存在且不等于零
(注:无穷等比数列各项的和即当 时该无穷数列前n项和的极限)
时该无穷数列前n项和的极限)
解: (Ⅰ)依题意可知,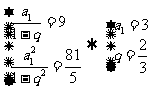
(Ⅱ)由(Ⅰ)知,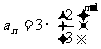 ,所以数列
,所以数列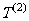 的的首项为
的的首项为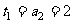 ,公差
,公差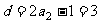 ,
,
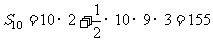 ,即数列
,即数列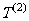 的前10项之和为155
的前10项之和为155
(Ⅲ)
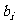 =
=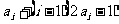 =
=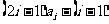 =
= ,
,
 ,
,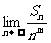 =
=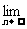
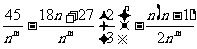
当m=2时,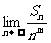 =-
=-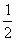 ,当m>2时,
,当m>2时,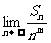 =0,所以m=2
=0,所以m=2
9. (2003年北京)如图,在边长为l的等边△ABC中,圆O1为△ABC的内切圆,圆O2与圆O1外切,且与AB、BC相切,…,圆On+1与圆On外切,且与AB、BC相切,如此无限继续下去,记圆On的面积为an(n∈N*).
(1)证明{an}是等比数列;
(2)求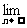 (a1+a2+…+an)的值.
(a1+a2+…+an)的值.
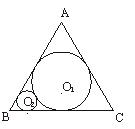

(1)证明:记rn为圆On的半径,
则r1=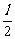 tan30°=
tan30°=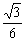 l.
l.
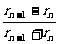 =sin30°=
=sin30°=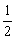 ,∴rn=
,∴rn=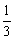 rn-1(n≥2).
rn-1(n≥2).
于是a1=πr12=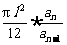 ,
,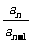 =(
=(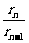 )2=
)2=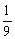 ,
,
∴{an}成等比数列.
(2)解:因为an=(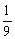 )n-1·a1(n∈N*),
)n-1·a1(n∈N*),
所以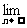 (a1+a2+…+an)=
(a1+a2+…+an)=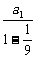 =
=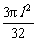 .
.
8.已知数列{an}、{bn}都是无穷等差数列,其中a1=3,b1=2,b2是a2与a3的等差中项,且
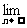
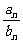 =
=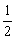 ,求极限
,求极限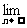 (
(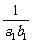 +
+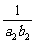 +…+
+…+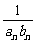 )的值.
)的值.
解:{an}、{bn}的公差分别为d1、d2.
∵2b2=a2+a3,即2(2+d2)=(3+d1)+(3+2d1),
∴2d2-3d1=2.
又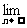
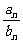 =
=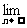
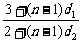 =
=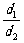 =
=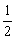 ,即d2=2d1,
,即d2=2d1,
∴d1=2,d2=4.
∴an=a1+(n-1)d1=2n+1,bn=b1+(n-1)d2=4n-2.
∴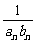 =
=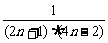 =
=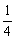 (
(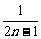 -
-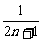 ).
).
∴原式=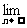
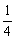 (1-
(1-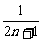 )=
)=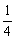 .
.
7. 求下列极限:
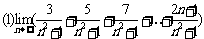 ;
;
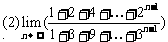
解:(1) 
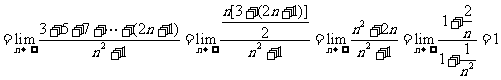 (2)
(2)
4. 2; 5.2; 6.3.
[解答题]
3.2(a1+a2+…+an)
=a1+[(a1+a2)+(a2+a3)+…+(an-1+an)]+an
=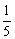 +[
+[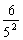 +
+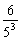 +…+
+…+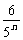 ]+an.
]+an.
∴原式=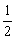 [
[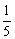 +
+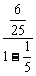 +
+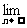 an]
an]
=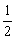 (
(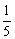 +
+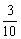 +
+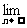 an).
an).
∵an+an+1=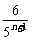 ,∴
,∴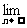 an+
an+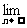 an+1=0.
an+1=0.
∴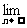 an=0.答案:C
an=0.答案:C
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com