
2.
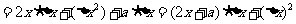

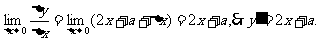
说明:求导其本质是求极限,在求极限的过程中,力求使所求极限的结构形式转化为已知极限的形式,即导数的定义,这是能够顺利求导的关键,因此必须深刻理解导数的概念.
证明函数的在一点处连续
例
证明:若函数 在点
在点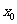 处可导,则函数
处可导,则函数 在点
在点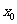 处连续.
处连续.
分析:从已知和要证明的问题中去寻求转化的方法和策略,要证明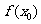 在点
在点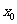 处连续,必须证明
处连续,必须证明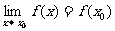 .由于函数
.由于函数 在点
在点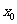 处可导,因此,根据函数在点
处可导,因此,根据函数在点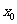 处可导的定义,逐步实现两个转化,一个是趋向的转化,另一个是形式(变为导数定义形式)的转化.
处可导的定义,逐步实现两个转化,一个是趋向的转化,另一个是形式(变为导数定义形式)的转化.
解:证法一:设 ,则当
,则当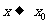 时,
时,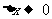 ,
,


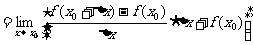
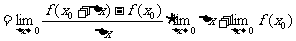
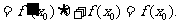
∴函数 在点
在点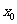 处连续.
处连续.
证法二:∵函数 在点
在点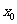 处可导,
处可导,
∴在点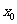 处有
处有
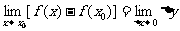
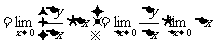

∴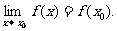 ∴函数
∴函数 在点
在点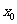 处连续.
处连续.
说明:对于同一个问题,可以从不同角度去表述,关键是要透过现象看清问题的本质,正确运用转化思想来解决问题.函数 在点
在点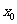 处连续,有极限以及导数存在这三者之间的关系是:导数存在
处连续,有极限以及导数存在这三者之间的关系是:导数存在 连续
连续 有极限.反之则不一定成立.证题过程中不能合理实现转化,而直接理解为
有极限.反之则不一定成立.证题过程中不能合理实现转化,而直接理解为 是使论证推理出现失误的障碍.
是使论证推理出现失误的障碍.
2.求函数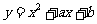 (a、b为常数)的导数.
(a、b为常数)的导数.
分析:根据导数的概念求函数的导数是求导数的基本方法,确定函数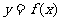 在
在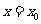 处的导数有两种方法,应用导数定义法和导函数的函数值法.
处的导数有两种方法,应用导数定义法和导函数的函数值法.
解:1.解法一(导数定义法):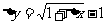 ,
,
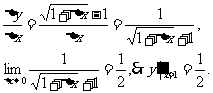
解法二(导函数的函数值法): ,
,

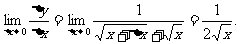
∴
3.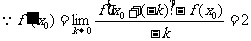 (含
(含 ),
),
∴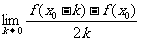

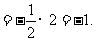 故选A.
故选A.
说明:概念是分析解决问题的重要依据,只有熟练掌握概念的本质属性,把握其内涵与外延,才能灵活地应用概念进行解题,不能准确分析和把握给定的极限式与导数的关系,盲目套用导数的定义是使思维受阻的主要原因.解决这类问题的关键就是等价变形,使问题转化.
利用定义求导数
例 1.求函数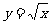 在
在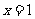 处的导数;
处的导数;
2.原式=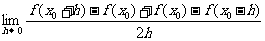

3.若 ,则
,则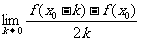 等于( )
等于( )
A.-1 B.-2
C.-1 D.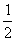
分析:在导数的定义中,增量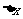 的形式是多种多样的,但不论
的形式是多种多样的,但不论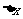 选择哪种形式,
选择哪种形式, 也必须选择相对应的形式.利用函数
也必须选择相对应的形式.利用函数 在点
在点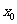 处可导的条件,可以将已给定的极限式班等变形转化为导数定义的结构形式.
处可导的条件,可以将已给定的极限式班等变形转化为导数定义的结构形式.
解:1.原式=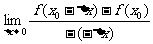

2.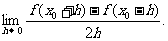
1. ;
;
2.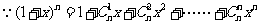
两边都是关于x的可导函数,求导得
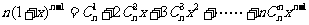 ,
,
令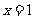 ,得
,得 ,
,
即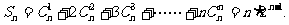
说明:通过对数列的通项进行联想,合理运用了逆向思维的方法,从而激发了思维的灵活性,使数列的求和问题获得解决,其关键是抓住了数列通项的形式结构.学生易犯的错误是受思维定式的影响不善于联想.
2.
分析:问题分别可通过错位相减的方法及构造二项式定理的方法来解决.转换思维角度,由求导公式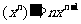 ,可联想到它们是另外一个和式的导数,因此可转化求和,利用导数运算可使问题解法更加简洁明快.
,可联想到它们是另外一个和式的导数,因此可转化求和,利用导数运算可使问题解法更加简洁明快.
解:1.当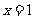 时,
时,

当 时,
时,
 ,
,
两边都是关于x的函数,求导得
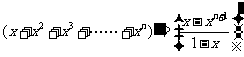 ,
,
即
1.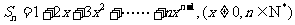
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com