
2.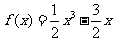 ,∴
,∴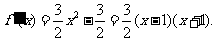
当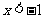 或
或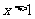 时,
时,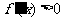 ,当
,当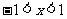 时,
时,
∴函数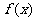 在
在 和
和 上是增函数,在(-1,1)上是减函数.
上是增函数,在(-1,1)上是减函数.
∴当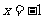 时,函数取得极大值
时,函数取得极大值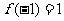 ,
,
当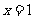 时,函数取得极小值
时,函数取得极小值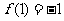 .
.
说明:解题的成功要靠正确思路的选择.本题从逆向思维的角度出发,根据题设结构进行逆向联想,合理地实现了问题的转化,使抽象的问题具体化,在转化的过程中充分运用了已知条件确定了解题的大方向.可见出路在于“思想认识”.在求导之后,不会应用 的隐含条件,因而造成了解决问题的最大思维障碍.
的隐含条件,因而造成了解决问题的最大思维障碍.
2.试判断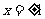 是函数的极小值还是极大值,并说明理由.
是函数的极小值还是极大值,并说明理由.
分析:考察函数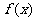 是实数域上的可导函数,可先求导确定可能的极值点,再通过极值点与导数的关系,即极值点必为
是实数域上的可导函数,可先求导确定可能的极值点,再通过极值点与导数的关系,即极值点必为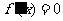 的根建立起由极值点
的根建立起由极值点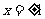 所确定的相关等式,运用待定系数法求出参数a、b、c的值.
所确定的相关等式,运用待定系数法求出参数a、b、c的值.
解:1.解法一: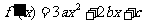 .
.
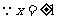 是函数
是函数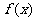 的极值点,
的极值点,
∴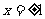 是方程
是方程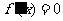 ,即
,即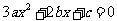 的两根,
的两根,
由根与系数的关系,得
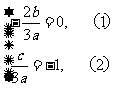
又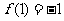 ,∴
,∴ , (3)
, (3)
由(1)、(2)、(3)解得 .
.
解法二:由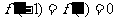 得
得
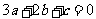 , (1)
, (1)
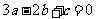 (2)
(2)
又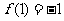 ,∴
,∴ , (3)
, (3)
解(1)、(2)、(3)得 .
.
1.试求常数a、b、c的值;
2.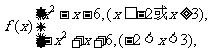
∴
令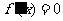 ,得
,得 .
.
当 或
或 时,
时,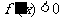 ,
,
∴函数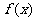 在
在 和
和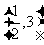 上是减函数;
上是减函数;
当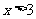 或
或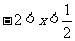 时,
时,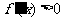 ,
,
∴函数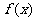 在
在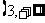 和
和 上是增函数.
上是增函数.
∴当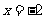 和
和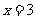 时,函数
时,函数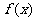 有极小值0,
有极小值0,
当 时,函数有极大值
时,函数有极大值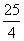 .
.
说明:在确定极值时,只讨论满足 的点附近的导数的符号变化情况,确定极值是不全面的.在函数定义域内不可导的点处也可能存在极值.本题1中
的点附近的导数的符号变化情况,确定极值是不全面的.在函数定义域内不可导的点处也可能存在极值.本题1中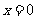 处,2中
处,2中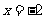 及
及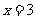 处函数都不可导,但
处函数都不可导,但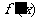 在这些点处左右两侧异号,根据极值的判定方法,函数
在这些点处左右两侧异号,根据极值的判定方法,函数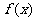 在这些点处仍取得极值.从定义分析,极值与可导无关.
在这些点处仍取得极值.从定义分析,极值与可导无关.
根据函数的极值确定参数的值
例 已知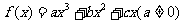 在
在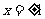 时取得极值,且
时取得极值,且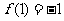 .
.
1.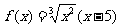 ;2.
;2.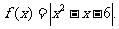
分析:利用求导的方法,先确定可能取到极值的点,然后依据极值的定义判定.在函数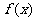 的定义域内寻求可能取到极值的“可疑点”,除了确定其导数为零的点外,还必须确定函数定义域内所有不可导的点.这两类点就是函数
的定义域内寻求可能取到极值的“可疑点”,除了确定其导数为零的点外,还必须确定函数定义域内所有不可导的点.这两类点就是函数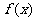 在定义内可能取到极值的全部“可疑点”.
在定义内可能取到极值的全部“可疑点”.
解:1.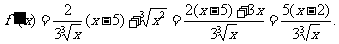
令 ,解得
,解得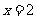 ,但
,但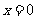 也可能是极值点.
也可能是极值点.
当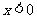 或
或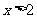 时,
时,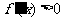 ,
,
∴函数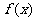 在
在 和
和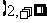 上是增函数;
上是增函数;
当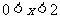 时,
时,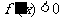 ,
,
∴函数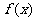 在(0,2)上是减函数.
在(0,2)上是减函数.
∴当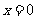 时,函数取得极大值
时,函数取得极大值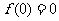 ,
,
当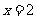 时,函数取得极小值
时,函数取得极小值 .
.
3.函数的定义域为R.
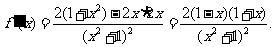
令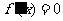 ,得
,得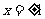 .
.
当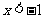 或
或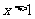 时,
时,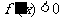 ,
,
∴函数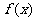 在
在 和
和 上是减函数;
上是减函数;
当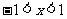 时,
时,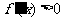 ,
,
∴函数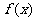 在(-1,1)上是增函数.
在(-1,1)上是增函数.
∴当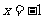 时,函数取得极小值
时,函数取得极小值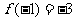 ,
,
当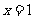 时,函数取得极大值
时,函数取得极大值
说明:思维的周密性是解决问题的基础,在解题过程中,要全面、系统地考虑问题,注意各种条件 综合运用,方可实现解题的正确性.解答本题时应注意 只是函数
只是函数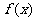 在
在 处有极值的必要条件,如果再加之
处有极值的必要条件,如果再加之 附近导数的符号相反,才能断定函数在
附近导数的符号相反,才能断定函数在 处取得极值.反映在解题上,错误判断极值点或漏掉极值点是学生经常出现的失误.
处取得极值.反映在解题上,错误判断极值点或漏掉极值点是学生经常出现的失误.
复杂函数的极值
例 求下列函数的极值:
2.函数定义域为R.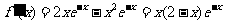
令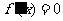 ,得
,得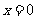 或
或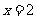 .
.
当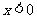 或
或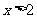 时,
时,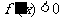 ,
,
∴函数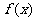 在
在 和
和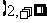 上是减函数;
上是减函数;
当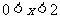 时,
时,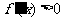 ,
,
∴函数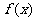 在(0,2)上是增函数.
在(0,2)上是增函数.
∴当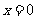 时,函数取得极小值
时,函数取得极小值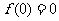 ,
,
当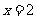 时,函数取得极大值
时,函数取得极大值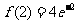 .
.
1.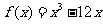 ;2.
;2.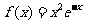 ;3.
;3.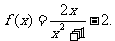
分析:按照求极值的基本方法,首先从方程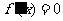 求出在函数
求出在函数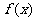 定义域内所有可能的极值点,然后按照函数极值的定义判断在这些点处是否取得极值.
定义域内所有可能的极值点,然后按照函数极值的定义判断在这些点处是否取得极值.
解:1.函数定义域为R.
令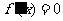 ,得
,得 .
.
当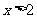 或
或 时,
时,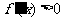 ,
,
∴函数在 和
和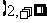 上是增函数;
上是增函数;
当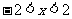 时,
时,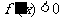 ,
,
∴函数在(-2,2)上是减函数.
∴当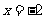 时,函数有极大值
时,函数有极大值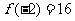 ,
,
当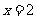 时,函数有极小值
时,函数有极小值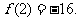
4.函数定义域为 ,当
,当 时,
时,
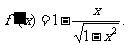
令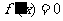 ,解得
,解得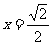 ,∴
,∴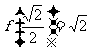 ,
,
又 ,∴
,∴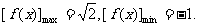
说明:对于闭区间 上的连续函数,如果在相应开区间
上的连续函数,如果在相应开区间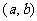 内可导,求
内可导,求 上最值可简化过程,即直接将极值点与端点的函数值比较,即可判定最大(或最小)的函数值,就是最大(或最小)值.解决这类问题,运算欠准确是普遍存在的一个突出问题,反映出运算能力上的差距.运算的准确要依靠运算方法的合理与简捷,需要有效的检验手段,只有全方位的“综合治理”才能在坚实的基础上形成运算能力,解决运算不准确的弊病.
上最值可简化过程,即直接将极值点与端点的函数值比较,即可判定最大(或最小)的函数值,就是最大(或最小)值.解决这类问题,运算欠准确是普遍存在的一个突出问题,反映出运算能力上的差距.运算的准确要依靠运算方法的合理与简捷,需要有效的检验手段,只有全方位的“综合治理”才能在坚实的基础上形成运算能力,解决运算不准确的弊病.
求两变量乘积的最大值
例 已知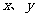 为正实数,且满足关系式
为正实数,且满足关系式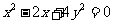 ,求
,求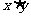 的最大值.
的最大值.
分析:题中有两个变量x和y,首先应选择一个主要变量,将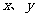 表示为某一变量(x或y或其它变量)的函数关系,实现问题的转化,同时根据题设条件确定变量的取值范围,再利用导数(或均值不等式等)求函数的最大值.
表示为某一变量(x或y或其它变量)的函数关系,实现问题的转化,同时根据题设条件确定变量的取值范围,再利用导数(或均值不等式等)求函数的最大值.
解:解法一: ,
,
∴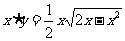 .
.
由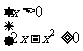 解得
解得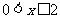 .
.
设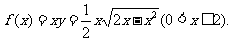
当 时,
时,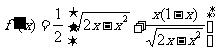
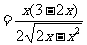 .
.
令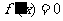 ,得
,得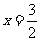 或
或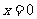 (舍).
(舍).
∴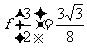 ,又
,又 ,∴函数
,∴函数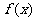 的最大值为
的最大值为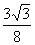 .
.
即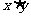 的最大值为
的最大值为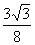 .
.
解法二:由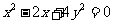 得
得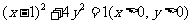 ,
,
设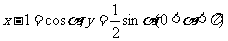 ,
,
∴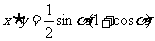 ,设
,设 ,
,
则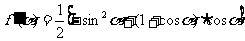
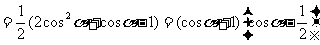
令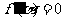 ,得
,得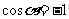 或
或 .
.
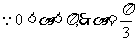 ,此时
,此时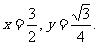
∴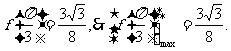
即当 时,
时,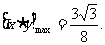
说明:进行一题多解训练,是一种打开思路,激发思维,巩固基础,沟通联系的重要途径,但要明确解决问题的策略、指向和思考方法,需要抓住问题的本质,领悟真谛,巧施转化,方可快捷地与熟悉的问题接轨,在实现转化的过程中,关键是要注意变量的取值范围必须满足题设条件,以免解题陷于困境,功亏一篑.
3.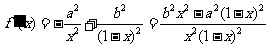 .
.
令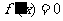 ,即
,即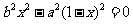 ,解得
,解得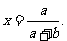
当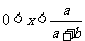 时,
时,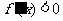 ,当
,当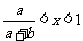 时,
时,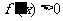 .
.
∴函数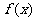 在点
在点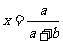 处取得极小值,也是最小值为
处取得极小值,也是最小值为
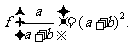 即
即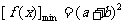 .
.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com