
10.(1994全国)如图,已知A1B1C1-ABC是正三棱柱,D是AC中点.
(1)证明AB1∥平面DBC1;
(2)假设AB1⊥BC1,求以BC1为棱,
DBC1与CBC1为面的二面角α的度数.
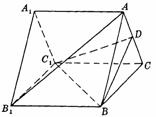
(1)证明:∵A1B1C1-ABC是正三棱柱,∴四边形B1BCC1是矩形.
连结B1C交BC1于E,则B1E=EC.连结DE.
在△AB1C中,∵AD=DC,∴DE∥AB1.
又AB1 平面DBC1,DE
平面DBC1,DE 平面DBC1,∴AB1∥平面DBC1.
平面DBC1,∴AB1∥平面DBC1.
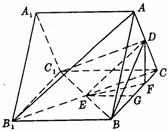 (2)解:作DF⊥BC,垂足为F,则DF⊥面B1BCC1,连结EF,则EF
(2)解:作DF⊥BC,垂足为F,则DF⊥面B1BCC1,连结EF,则EF
是ED在平面B1BCC1上的射影.
∵AB1⊥BC1,
由(1)知AB1∥DE,∴DE⊥BC1,则BC1⊥EF,∴∠DEF是二面角α的平面角.
设AC=1,则DC=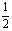 .∵△ABC是正三角形,
.∵△ABC是正三角形,
∴在Rt△DCF中,DF=DC·sinC=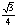 ,
,
CF=DC·cosC=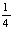 .取BC中点G.
.取BC中点G.
∵EB=EC,∴EG⊥BC.在Rt△BEF中,
EF2=BF·GF,又BF=BC-FC=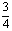 ,GF=
,GF=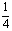 ,
,
∴EF2=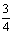 ·
·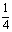 ,即EF=
,即EF=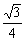 .
.
∴tg∠DEF=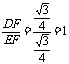 .
.
∴∠DEF=45°故二面角α为45°.
[探索题]
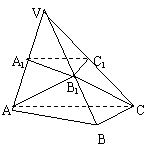
9.如图,三棱锥V-ABC中,VA⊥底面ABC,
∠ABC=90°.
(1)求证:V、A、B、C四点在同一球面上;
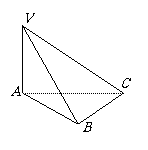 (2)过球心作一平面与底面内直线AB垂直,求证:此平面截三棱锥所得的截面是矩形.
(2)过球心作一平面与底面内直线AB垂直,求证:此平面截三棱锥所得的截面是矩形.
证明:(1)取VC的中点M,
∵VA⊥底面ABC,∠ABC=90°,
∴BC⊥VB.在Rt△VBC中,M为斜边VC的中点,
∴MB=MC=MV.同理,在Rt△VAC中,MA=MV=MC.
∴MV=MC=MA=MB.
∴V、A、B、C四点在同一圆面上,M是球心.
(2)取AC、AB、VB的中点分别为N、P、Q,连结NP、PQ、QM、MN,则MNPQ就是垂直于AB的三棱锥V-ABC的截面,易证PQMN是平行四边形.又VA⊥BC,QP∥VA,NP∥BC,∴QP⊥PN.故截面MNPQ是矩形.
8.已知三棱锥S-ABC的三条侧棱SA、SB、SC两两互相垂直且长度分别为a、b、c,设O为S在底面ABC上的射影.求证:
(1)O为△ABC的垂心;
(2)O在△ABC内;
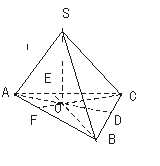

(3)设SO=h,则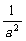 +
+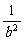 +
+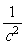 =
=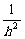 .
.
证明:(1)∵SA⊥SB,SA⊥SC,
∴SA⊥平面SBC,BC 平面SBC.∴SA⊥BC.
平面SBC.∴SA⊥BC.
而AD是SA在平面ABC上的射影,∴AD⊥BC.
同理可证AB⊥CF,AC⊥BE,故O为△ABC的垂心.
(2)证明△ABC为锐角三角形即可.不妨设a≥b≥c,则底面三角形ABC中,AB=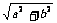 为最大,从而∠ACB为最大角.
为最大,从而∠ACB为最大角.
用余弦定理求得:cos∠ACB=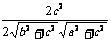 >0,
>0,
∴∠ACB为锐角,△ABC为锐角三角形.故O在△ABC内.
(3)SB·SC=BC·SD,
故SD=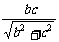 ,
,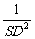 =
= 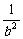 +
+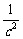 ,
,
又SA·SD=AD·SO,
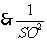 =
=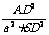 =
=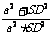
=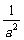 +
+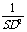 =
= 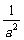 +
+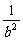 +
+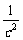 =
=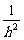 .
.
7. (2006山东)如图,已知平面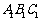 平行于三棱锥
平行于三棱锥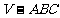 的底面ABC,等边△
的底面ABC,等边△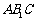 所在的平面与底面ABC垂直,且∠ACB=90°,设
所在的平面与底面ABC垂直,且∠ACB=90°,设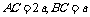
(1)求证直线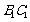 是异面直线
是异面直线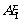 与
与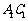 的公垂线;
的公垂线;
(2)求点A到平面VBC的距离;
(3)求二面角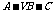 的大小.
的大小.

证明(Ⅰ)∵平面
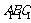 ∥平面
∥平面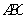 ,
,
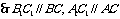
∵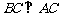 ∴
∴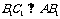
又∵平面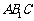 ⊥平面
⊥平面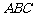 ,平面
,平面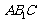 ∩平面
∩平面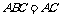 ,∴
,∴ ⊥平面
⊥平面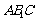 ,
,
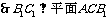
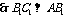 ,
,
又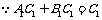 ,
,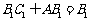 .
.
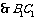 为
为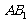 与
与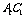 的公垂线.
的公垂线.
解(Ⅱ):过A作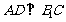 于D,
于D,
∵△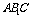 为正三角形,∴D为
为正三角形,∴D为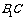 的中点.
的中点.
∵BC⊥平面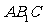 ∴
∴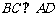 ,
,
又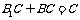 ,∴AD⊥平面
,∴AD⊥平面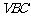 ,
,
∴线段AD的长即为点A到平面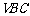 的距离.
的距离.
在正△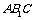 中,
中,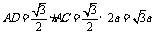 .
.
∴点A到平面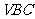 的距离为
的距离为 .
.
解法2:取AC中点O连结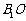 ,则
,则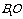 ⊥平面
⊥平面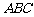 ,且
,且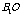 =
=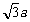 .
.
由(Ⅰ)知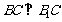 ,设A到平面
,设A到平面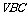 的距离为x,
的距离为x,
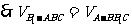 ,
,
即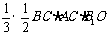
 ,
,
解得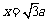 .即A到平面
.即A到平面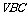 的距离为
的距离为 .
.
则
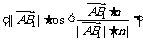
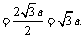
∴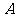 到平面
到平面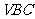 的距离为
的距离为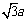 .
.
(III)过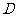 点作
点作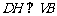 于
于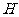 ,连
,连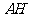 ,由三重线定理知
,由三重线定理知
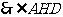 是二面角
是二面角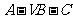 的平面角.
的平面角.
在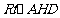 中,
中,
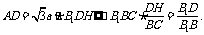
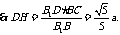
 .
.
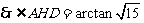 .
.
所求二面角大小为arctan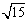 .
.
5. 4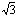 192π; 6.距离为12.
192π; 6.距离为12.
[解答题]
6.已知球面上的三点A、B、C,AB=6,BC=8,AC=10,球的半径为13,则球心到平面ABC的距离为 .
◆答案提示: 1-3.ACC; 4. 1∶3∶5;
5.(2004年北京)地球仪上北纬30°纬线的长度为12πcm,该地球仪的半径是_________cm,表面积是_________cm2.
4.过棱锥高的三等分点作两个平行于底面的截面,它们将棱锥的侧面分成三部分的面积的比(自上而下)为__________.
3.各顶点都在一个球面上的正四棱柱高为4,体积为16,则这个球的表面积是( )
A.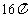 B.
B.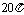 C.
C.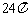 D.
D.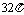
[填空题]
2.长方体的一个顶点上三条棱长为3、4、5,且它的八个顶点都在一个球面上,这个球的表面积是 ( )
A.20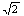 π B.25
π B.25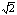 π C.50π D.200π
π C.50π D.200π
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com