(15)(本小题满分12分)

已知直线：y＝3x+3，求：(1)直线关于点M(3，2)对称的直线方程；

(2)直线x－y－2＝0关于直线对称的直线方程。

(16)(本小题满分12分)

　　 　　设命题函数是上的减函数，命题函数 在

的值域为．若“且”为假命题，“或”为真命题，求的取值范围．

(17)(本小题满分14分)

设函数(其中)，且的图像在轴右侧的第一个最高点的横坐标为．

　　 (1)求的值；　

　　 (2)如果在区间上的最小值为，求的值．

(18)(本小题满分16分)烟囱向其周围地区散落烟尘而造成环境污染．已知、两座烟囱相距，其中烟囱喷出的烟尘量是烟囱的倍，经环境检测表明：落在地面某处的烟尘浓度与该处到烟囱距离的平方成反比，而与烟囱喷出的烟尘量成正比．(比例系数为)．若是连接两烟囱的线段上的点(不包括端点)，设，点的烟尘浓度记为．

(1)写出关于的函数表达式；

(2)是否存在这样的点，使该点的烟尘浓度最低？若存在，求出的距离；若不存在，说明理由．

(19)(本小题满分16分)已知函数的图象与轴分别相交于点A、B，(分别是与轴正半轴同方向的单位向量)，函数.

(1)求的值；(2)当满足时，求函数的最小值.

(20)(本小题满分16分)

　　　 有以下真命题：设，，…，是公差为的等差数列中的任意个项，若(，、、或)①，则有②，特别地，当时，称为，，…，的等差平均项．

(1)当，时，试写出与上述命题中的(1)，(2)两式相对应的等式；

(2)已知等差数列的通项公式为，试根据上述命题求，，，

的等差平均项；

(3)试将上述真命题推广到各项为正实数的等比数列中，写出相应的真命题．

(1)命题“”的否定是　　　　　　　　 ．

(2)“”是“”的　　 　　　　条件

(3)若均为锐角， 则　　 　　　　

(4) 　　　　．

(5)在中，，面积，则等于　　 　　　

(6)已知，则，则等于　　 　　　

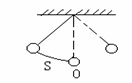
(7)如图，单摆从某点开始来回摆动，离开平衡位置O的

距离S厘米和时间秒的函数关系为：，

那么单摆来回摆动一次所需的时间为 　　　秒．

(8)函数(为常数)是偶函数，且在上是减函数，则整数的值是　　 　．

(9)已知集合，，若,则实数的取值范围是　 　　　．

(10)定义在上的偶函数，满足，且在上是减函数．下面五个关于的命题中，命题正确的个数有　　 　　　

①是周期函数；②的图像关于对称；③在上是减函数；④在上为增函数；⑤．

(11)给出下列命题：①若函数，则；②若函数，图像上及邻近点， 则；③加速度是动点位移函数对时间的导数；④，则．其中正确的命题为　 　　　　．(写上序号)

(12)对，记，函数的最大值为　 　　．

(13)在直角坐标系中，的三个顶点坐标分别为,动点是内的点(包括边界)．若目标函数的最大值为，且此时的最优解所确定的点是线段上的所有点，则目标函数的最小值为　 　　　．

(14)甲用元买入一种股票，后将其转卖给乙，获利，而后乙又将这些股票卖给甲，乙损失了，最后甲按乙卖给甲的价格九折将股票售出,甲在上述交易中盈利　　　 元．

随着李阳 “疯狂英语”讲师团的到来和校园 “英语周”活动的开展，我校学生学英语的积极性空前高涨.你最近以访谈的形式对高三年级的学生做了一次调查，请根据下图所示调查结果, 用英语写一篇150词左右的短文, 作简单的原因分析并谈谈个人看法。

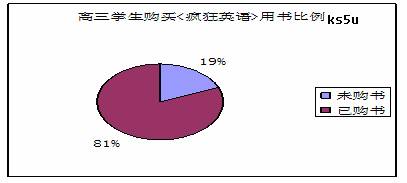
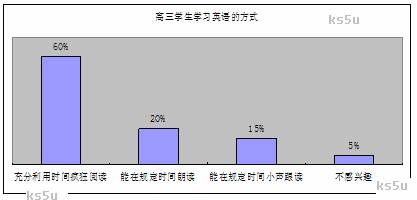
注意: 短文的标题及首句已为你写好,不计入总词数。

　 Recently, with the English Week Activities being held in our school, more and more students have shown great interest in English reading.　

15. Whom was it up to ________ the matter?

A. decide　　　　　 B. to decide　　　　 C. deciding　　　　　 D. decided