
5.
已知点P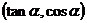 在第三象限,则角
在第三象限,则角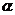 的终边在第
的终边在第 象限.
象限.
讲解 由已知得
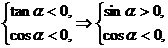

从而角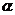 的终边在第二象限,故应填二.
的终边在第二象限,故应填二.
4.
果函数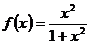 ,那么
,那么
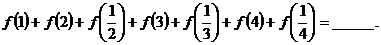

讲解 容易发现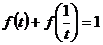 ,这就是我们找出的有用的规律,于是
,这就是我们找出的有用的规律,于是
原式=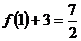 ,应填
,应填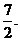

本题是2002年全国高考题,十分有趣的是,2003年上海春考题中也有一道类似题:
设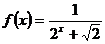 ,利用课本中推导等差数列前n项和的公式的方法,可求得
,利用课本中推导等差数列前n项和的公式的方法,可求得


3. 若函数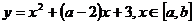 的图象关于直线
的图象关于直线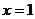 对称,则
对称,则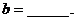

讲解 由已知抛物线的对称轴为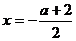 ,得
,得 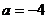 ,而
,而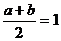 ,有
,有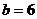 ,故应填6.
,故应填6.
1 已知函数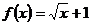 ,则
,则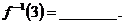

讲解 由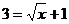 ,得
,得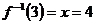 ,应填4.
,应填4.
请思考为什么不必求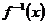 呢?
呢?
2.
集合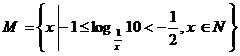 的真子集的个数是
的真子集的个数是

讲解 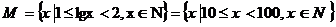 ,显然集合M中有90个元素,其真子集的个数是
,显然集合M中有90个元素,其真子集的个数是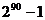 ,应填
,应填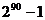 .
.
快速解答此题需要记住小结论;对于含有n个元素的有限集合,其真子集的个数是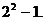

通过“化复杂为简单、化陌生为熟悉”,将问题等价地转化成便于解决的问题,从而得出正确的结果.
例10 不等式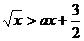 的解集为(4,b),则a=
,b=
.
的解集为(4,b),则a=
,b=
.
解:设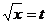 ,则原不等式可转化为:
,则原不等式可转化为: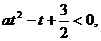 ∴a > 0,且2与
∴a > 0,且2与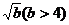 是方程
是方程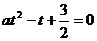 的两根,由此可得:
的两根,由此可得: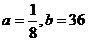 .
.
例11 不论k为何实数,直线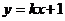 与曲线
与曲线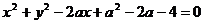 恒有交点,则实数a的取值范围是 .
恒有交点,则实数a的取值范围是 .
解:题设条件等价于点(0,1)在圆内或圆上,或等价于点(0,1)到圆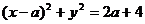 ,∴
,∴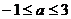 .
.
例12 函数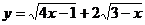 单调递减区间为
.
单调递减区间为
.
解:易知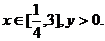 ∵y与y2有相同的单调区间,而
∵y与y2有相同的单调区间,而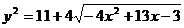 ,∴可得结果为
,∴可得结果为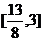 .
.
总之,能够多角度思考问题,灵活选择方法,是快速准确地解数学填空题的关键.

对于一些含有几何背景的填空题,若能数中思形,以形助数,则往往可以简捷地解决问题,得出正确的结果.
例7
如果不等式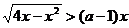 的解集为A,且
的解集为A,且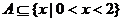 ,那么实数a的取值范围是
.
,那么实数a的取值范围是
.
解:根据不等式解集的几何意义,作函数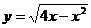 和
和
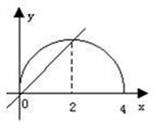 函数
函数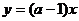 的图象(如图),从图上容易得出实数a的取
的图象(如图),从图上容易得出实数a的取
值范围是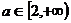 .
.
例8 求值 .
.
解:

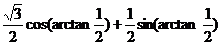 ,
,
构造如图所示的直角三角形,则其中的角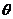 即为
即为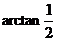 ,从而
,从而
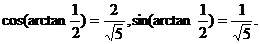 所以可得结果为
所以可得结果为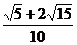 .
.
例9 已知实数x、y满足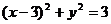 ,则
,则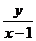 的最大值是
.
的最大值是
.
解: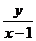 可看作是过点P(x,y)与M(1,0)的直线的斜率,其中点P的圆
可看作是过点P(x,y)与M(1,0)的直线的斜率,其中点P的圆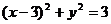 上,如图,当直线处于图中切线位置时,斜率
上,如图,当直线处于图中切线位置时,斜率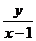 最大,最大值为
最大,最大值为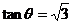 .
.
当填空题的结论唯一或题设条件中提供的信息暗示答案是一个定值时,可以把题中变化的不定量用特殊值代替,即可以得到正确结果.
例4 在△ABC中,角A、B、C所对的边分别为a、b、c。若a、b、c成等差数列,则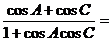 .
.
解:特殊化:令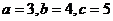 ,则△ABC为直角三角形,
,则△ABC为直角三角形,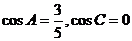 ,从而所求值为
,从而所求值为 .
.
例5 过抛物线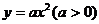 的焦点F作一直线交抛物线交于P、Q两点,若线段PF、FQ的长分别为p、q,则
的焦点F作一直线交抛物线交于P、Q两点,若线段PF、FQ的长分别为p、q,则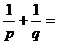 .
. 
分析:此抛物线开口向上,过焦点且斜率为k的直线与抛物线均有两个交点P、Q,当k变化时PF、FQ的长均变化,但从题设可以得到这样的信息:尽管PF、FQ不定,但其倒数和应为定值,所以可以针对直线的某一特定位置进行求解,而不失一般性.
解:设k = 0,因抛物线焦点坐标为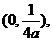 把直线方程
把直线方程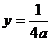 代入抛物线方程得
代入抛物线方程得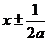 ,∴
,∴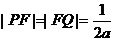 ,从而
,从而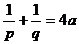 .
.
例6 求值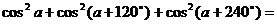 .
.
分析:题目中“求值”二字提供了这样信息:答案为一定值,于是不妨令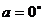 ,得结果为
,得结果为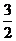 .
.
这是解填空题的基本方法,它是直接从题设条件出发、利用定义、定理、性质、公式等知识,通过变形、推理、运算等过程,直接得到结果.
例1设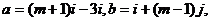 其中i,j为互相垂直的单位向量,又
其中i,j为互相垂直的单位向量,又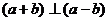 ,则实数m = .
,则实数m = .
解: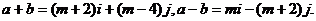 ∵
∵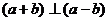 ,∴
,∴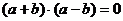 ∴
∴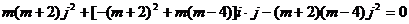 ,而i,j为互相垂直的单位向量,故可得
,而i,j为互相垂直的单位向量,故可得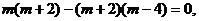 ∴
∴ .
.
例2已知函数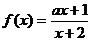 在区间
在区间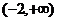 上为增函数,则实数a的取值范围是 .
上为增函数,则实数a的取值范围是 .
解: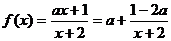 ,由复合函数的增减性可知,
,由复合函数的增减性可知,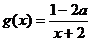 在
在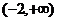 上为增函数,∴
上为增函数,∴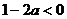 ,∴
,∴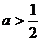 .
.
例3现时盛行的足球彩票,其规则如下:全部13场足球比赛,每场比赛有3种结果:胜、平、负,13长比赛全部猜中的为特等奖,仅猜中12场为一等奖,其它不设奖,则某人获得特等奖的概率为
.
解:由题设,此人猜中某一场的概率为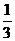 ,且猜中每场比赛结果的事件为相互独立事件,故某人全部猜中即获得特等奖的概率为
,且猜中每场比赛结果的事件为相互独立事件,故某人全部猜中即获得特等奖的概率为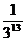 .
.
22.黄河、长江是中华文明的摇篮,是中华民族坚强不屈的象征。结合所学知识,完成下列问题:
(1)古代史上,黄河流域是农业文明与畜牧业文明的交汇区域,两大文明的冲突、融合伴随着黄河文明的发展。秦汉
时期为解决少数民族的威胁,中原政权各采取了哪些重大措施?
(2)南北朝以后,我国经济重心逐步南移。就黄河流域而言,这一地区逐渐丧失经济重心地位的原因有哪些?
(3)乐山大佛与敦煌莫高窟、龙门石窟分别是长江、黄河流域的著名文化遗产。归纳概括这些文化遗产所反映的文化特征。
答案 (1)秦朝:武力征伐匈奴,取得河套地区;修筑万里长城,抵御匈奴南下。
西汉:西汉初期实行和亲政策,汉武帝时进行军事反攻,后期友好交往。
东汉:两次反击匈奴,匈奴的威胁最后解除。
(2)原因:北方长期战乱,北民南迁;北方长期过度开发,生态环境恶化;政治重心南移。(答出其中两点即可)
(3)文化特征:文化繁荣;建筑雕刻艺术精湛;佛教盛行,影响深远;中外文化交流频繁。(答出其中两点即可)
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com