
2.二倍角公式


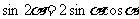 ;
;


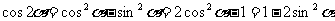 ;
;


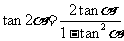 。
。


1.两角和与差的三角函数


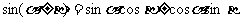 ;
;


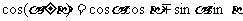 ;
;


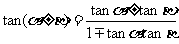 。
。


从近几年的高考考察的方向来看,这部分的高考题以选择、解答题出现的机会较多,有时候也以填空题的形式出现,它们经常与三角函数的性质、解三角形及向量联合考察,主要题型有三角函数求值,通过三角式的变换研究三角函数的性质.


本讲内容是高考复习的重点之一,三角函数的化简、求值及三角恒等式的证明是三角变换的基本问题。历年高考中,在考察三角公式的掌握和运用的同时,还注重考察思维的灵活性和发散性,以及观察能力、运算及观察能力、运算推理能力和综合分析能力.


3.能运用上述公式进行简单的恒等变换(包括引导导出积化和差、和差化积、半角公式,但不要求记忆)。


2.能从两角差的余弦公式导出两角和与差的正弦、余弦、正切公式,二倍角的正弦、余弦、正切公式,了解它们的内在联系;


1.经历用向量的数量积推导出两角差的余弦公式的过程,进一步体会向量方法的作用;


18.解析:(1)这是一个相对论速度变换问题。取地球为S系,飞船为S′系,向东为x轴正向。则S′系相对S系的速度v=0.60c,彗星相对S系的速度ux=-0.80c。由速度变换可得所求结果。结果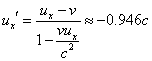
即彗星以0.946c的速率向飞船靠近。
(2)由时间间隔的相对性有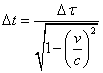 =5.0s
=5.0s
解得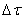 =4.0s。
=4.0s。
答案:(1)-0.946c (2)4.0 s
17.解析:设杆固有长度为l0,在K′系中,x′方向:l0x=l0
cosα′,y′方向:l0y=l0sina′,由长度的相对性得x′方向: 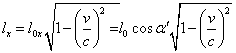
y′方向:ly=l0y=l0sina′。
因此在K系中观测时: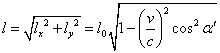
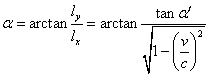
代入数据解得:l=4.79 m;a=31.490
可见,长度不但缩短,空间方位也要变化。
答案:4.79 m 31.490
16.设恒星为K系,飞船A为K′系,并沿x轴正方向运动,取飞船B为研究对象,沿x轴负方向运动。
飞船B在K′系中的速度为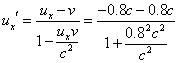 =
=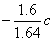
问题得证。
15.4.27s 3.66×108m 4.07s
解析:设地球和月球位于K 系x轴,地球于O、月球于L0处,飞船为K′系,相对K系以速度v沿x轴正向运动。
地球上的时钟显示的旅行时间为Δt=L0/v≈4.27s
在飞船上测量地、月距离L时,K系的 L0是固有长度,由“长度收缩”效应: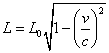 ≈3.66×108m
≈3.66×108m
飞船上的时钟显示的旅行时间为Δt′=L/v≈4.07s
Δt′<Δt,即“动钟变慢”,对于飞船而言,“离开地球”和“到达月球”两事件都发生在飞船上,所以飞船时钟显示的时间间隔是“固有时”。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com