
2. 函数及其性质考查更是高考函数试题的主干,是中学与大学数学相衔接的重要内容,是承上启下的必备知识,也是历年高考的热点.本考点每年必考。近年高考对函数知识的考查,除了保持函数各知识点比较高的覆盖面外,还强化了对函数本质和函数应用的考查,体现了函数知识考查的深度和广度,函数的概念的考察多数是与其它知识以综合题的形式出现,有关函数的综合题较难。
具体考查:
(1) 常见初等函数的图像及其性质,其中二次函数及其对数函数更为重要,属中档题;
(2) 考查函数与方程、不等式、三角、数列、曲线方程、导数(尤其要重视与导数的结合)等知识的交叉渗透及其应用,属中、高档题;
(3) 考查以函数为模型的实际应用题,让考生从数学角度观察事物、阐释现象,分析解决问题,属中档题;
(4) 变函数的具体形式为抽象形式,用以考查抽象思维水平,以及将抽象与具体进行相互转化的思维能力,可结合在函数的各种题型中进行考查。
[疑难点拔]
(解释重点、难点及知识体系,尤其是考试中学生常见错案分析。)
综合上述三年统计表可知本单元在高考中试题类型与特点有:
1. 集合、映射、简易逻辑、四种命题一般都是基本题,综合性题目少,且综合性的深度较小.解答题少.今年理科试题中没有出现本单元的解答题型.
22. 解: (1)由题意得: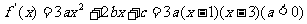
∴在(-∞,1)上,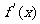 <0;
<0;
在(1,3)上,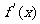 >0; 在3,+∞)上,
>0; 在3,+∞)上,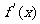 <0;
<0;
因此,f(x)在x0=1处取得极小值-4
∴a+b+c=-4 ①…
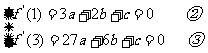
①②③联立得:
∴f(x)=-x3+6x2-9x
(2)由(1)知f(x)在x=3处取得极大值为:f(3)=0
(3)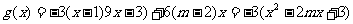
①当2≤m≤3时,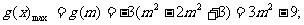
②当m<2时,g(x)在[2,3]上单调递减,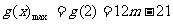
③当m>3时,g(x)在[2,3]上单调递增,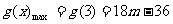
21. 解:(1)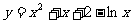 ,知x =1时,y
= 4,
,知x =1时,y
= 4,
又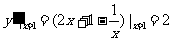
∴直线l的方程为y-4 = 2 (x-1),即y = 2x +2
又点(n-1,an+1-an-a1)在l上,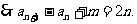
即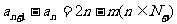
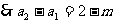
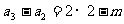
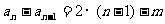
各项迭加,得
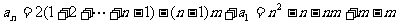
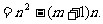
∴通式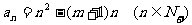
(2)∵m为奇数,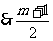 为整数,
为整数,
由题意,知a5是数列{an}中的最小项,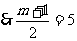
∴得m = 9
令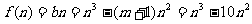
则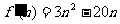 ,由
,由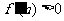 ,得
,得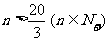
即为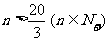 时,
时,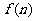 单调递增,即
单调递增,即 成立,
成立,
∴n的取值范围是n≥7,且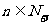
20. (1)由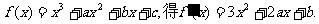
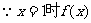 有极值,
有极值,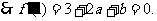 ①
①
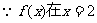 处的切线l的倾斜角为
处的切线l的倾斜角为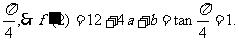 ②
②
由①②可解得a =-4,b = 5
设切线l的方程为y = x + m,由坐标原点(0,0)到切线l的距离为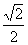 ,可得m =±1,
,可得m =±1,
又切线不过第四象限,所以m =1,切线方程为y = x + 1.
∴切点坐标为(2,3),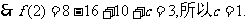
故a=-4,b = 5,c =1.
(2)由(Ⅰ)知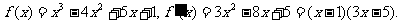
 ,∴函数
,∴函数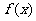 在区间[-1,1]上递增,在
在区间[-1,1]上递增,在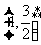 上递减,
上递减,
又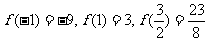 ,
,
∴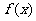 在区间
在区间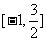 上的最大值为3,最小值为-9.
上的最大值为3,最小值为-9.
19. (1)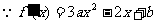 ,
,
又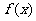 在区间(-∞,0)及(4,+∞)上都是增函数,在区间(0,4)上是减函数,
在区间(-∞,0)及(4,+∞)上都是增函数,在区间(0,4)上是减函数,
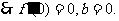
又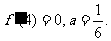
(2)
当x=1时,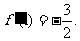
此时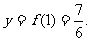
即切线的斜率为-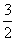 ,切点坐标为(1,
,切点坐标为(1,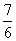 ), 所求切线方程为9x+6y-16=0.
), 所求切线方程为9x+6y-16=0.
至少有一件是次品的概率为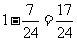
(2)设抽取n件产品作检验,则3件次品全部检验出的概率为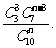
由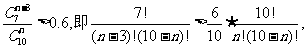 整理得:
整理得: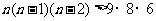 ,
,
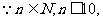 ∴当n=9或n=10时上式成立.
∴当n=9或n=10时上式成立.
答:任意取出3件产品作检验,其中至少有1件是次品的概率为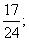 为了保证使3件次品全部检验出的概率超过0.6,最少应抽取9件产品作检验.
为了保证使3件次品全部检验出的概率超过0.6,最少应抽取9件产品作检验.
18. (1)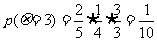
(2)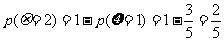
21. 设曲线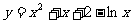 在x = 1处的切线为1,数列
在x = 1处的切线为1,数列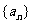 的首项
的首项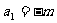 ,(其中常数m为正奇数)且对任意
,(其中常数m为正奇数)且对任意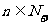 ,点
,点 均在直线上.
均在直线上.
(1)求出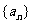 的通项公式;
的通项公式;
(2)令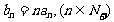 ,当
,当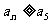 恒成立时,求出n的取值范围,使得
恒成立时,求出n的取值范围,使得 成立.
成立.
22已知函数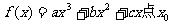 处的取得极小值-4,使其导函数
处的取得极小值-4,使其导函数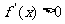 的x的取值范围为(1,3),求:
的x的取值范围为(1,3),求:
(1)f(x)的解析式;
(2)f(x)的极大值;
(3)x∈[2,3],求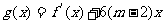 的最大值.
的最大值.
2007-2008学年度南昌市高三第一轮复习训练题
数学(十八) (文科·统计与导数)答案
20. 已知函数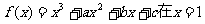 处有极值,
处有极值,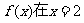 处的切线l不过第四象限且倾斜角为
处的切线l不过第四象限且倾斜角为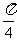 ,坐标原点到切线l的距离为
,坐标原点到切线l的距离为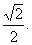
|
(2)求函数 上的最大值和最小值.
上的最大值和最小值.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com