
1、若函数 对任意实数
对任意实数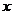 ,都有
,都有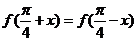 ,则
,则 等于
等于
A、0 B、3 C、-3 D、3或-3
例1、已知函数 。
。
(1)求它的振幅、周期和初相;
(2)用五点法作出它的图象;
(3)说明 的图象可由
的图象可由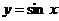 的图象经过怎样的变换而得到?
的图象经过怎样的变换而得到?
例2、把函数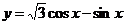 的图象向左平移
的图象向左平移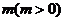 个单位,所得的图象关于
个单位,所得的图象关于 轴对称,求
轴对称,求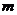 的最小值。
的最小值。
 例3、如图为
例3、如图为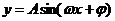
 的图象的一段,求其解析式。
的图象的一段,求其解析式。
例4、受日月的引力,海水会发生涨落,这种现象叫做潮汐,在通常情况下,船在涨潮时驶进航道,靠近船坞;缺货后落潮时返回海洋。某港口水的深度 (米)是时间
(米)是时间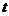 (
(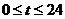 ,单位:时)的函数,记作
,单位:时)的函数,记作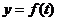 ,下面是该港口在某季节每天水深的数据:
,下面是该港口在某季节每天水深的数据:
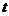 (时) (时) |
0 |
3 |
6 |
9 |
12 |
15 |
18 |
21 |
24 |
 (米) (米) |
10.0 |
13.0 |
9.9 |
7.0 |
10.0 |
13.0 |
10.1 |
7.0 |
10.0 |
经长期观察,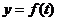 曲线可以近似地看做函数
曲线可以近似地看做函数 的图象。
的图象。
(1)
根据以上数据,求出函数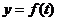 的近似表达式;
的近似表达式;
(2) 一般情况下,船舶航行时,船底离海底的距离为5米或5米以上时认为是安全的(船舶停靠时,船底只需不碰海底即可),某船吃水深度(船底离水面的距离)为6.5米。如果该船想在同一天内安全进出港,问它至多能在港内停留多长时间(忽略进出港所需的时间)?
例5.(00) 已知函数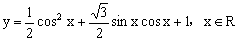
(I)当函数y取得最大值时,求自变量x的集合; (II)该函数的图象可由y=sinx(x∈R)的图象经过怎样的平移和伸缩变换得到?
6、方程 有___个实数根。
有___个实数根。
5、已知函数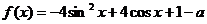 ,当
,当 时
时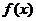 =0恒有解,则
=0恒有解,则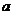 的范围是______。
的范围是______。
4、(00)函数y=-xcosx的部分图象是
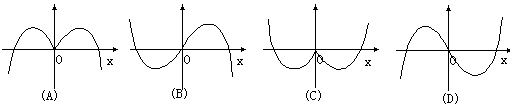
3、函数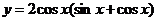 的图象一个对称中心的坐标是 ( )
的图象一个对称中心的坐标是 ( )
A、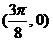 B、
B、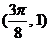 C、
C、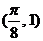 D、
D、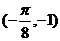
2、函数 的部分图象是 ( )
的部分图象是 ( )
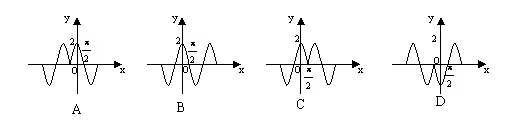
1、为了得到函数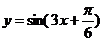 的图象,只需把函数
的图象,只需把函数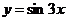 的图象 ( )
的图象 ( )
A、向左平移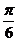 B、向左平移
B、向左平移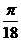 C、向右平移
C、向右平移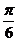 D、向右平移
D、向右平移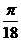
(二)三角函数图象的作法:
1.几何法(利用三角函数线)
2. 描点法:五点作图法(正、余弦曲线),三点二线作图法(正、余切曲线).
3.利用图象变换作三角函数图象.
三角函数的图象变换有振幅变换、周期变换和相位变换等,重点掌握函数y=Asin(ωx+φ)+B的作法.
函数y=Asin(ωx+φ)的物理意义:
振幅|A|,周期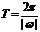 ,频率
,频率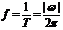 ,相位
,相位 初相
初相 (即当x=0时的相位).(当A>0,ω>0 时以上公式可去绝对值符号),
(即当x=0时的相位).(当A>0,ω>0 时以上公式可去绝对值符号),
(1)振幅变换或叫沿y轴的伸缩变换.(用y/A替换y)由y=sinx的图象上的点的横坐标保持不变,纵坐标伸长(当|A|>1)或缩短(当0<|A|<1)到原来的|A|倍,得到y=Asinx的图象.
(2)周期变换或叫做沿x轴的伸缩变换.(用ωx替换x)由y=sinx的图象上的点的纵坐标保持不变,横坐标伸长(0<|ω|<1)或缩短(|ω|>1)到原来的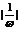 倍,得到y=sinω x的图象.
倍,得到y=sinω x的图象.
(3)相位变换或叫做左右平移.(用x+φ替换x)由y=sinx的图象上所有的点向左(当φ>0)或向右(当φ<0)平行移动|φ|个单位,得到y=sin(x+φ)的图象.
(4)上下平移(用y+(-b)替换y)由y=sinx的图象上所有的点向上(当b>0)或向下(当b<0)平行移动|b|个单位,得到y=sinx+b的图象.
注意:由y=sinx的图象利用图象变换作函数y=Asin(ωx+φ)+B(A>0,ω>0)(x∈R)的图象,要特别注意:当周期变换和相位变换的先后顺序不同时,原图象延x轴量伸缩量的区别。
 (一)熟悉.三角函数图象的特征:
(一)熟悉.三角函数图象的特征:
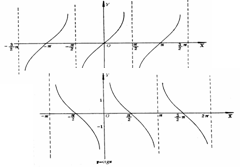 y=tanx
y=tanx
y=cotx
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com