
(三)我国气候特征: ① 大陆性季风气候显著
② 雨热同期
③ 气候复杂多样
西北终年比较干旱: 地处大陆内部 降水少
云贵高原多旱灾的地貌原因: 喀斯特地貌 地表水下渗严重
5、干湿地区(由蒸发量和降水量决定)
①四个干湿地区的大致范围
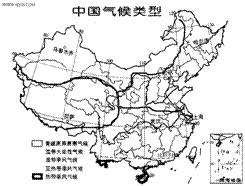 ②年等降水量线与农业类型的关系
②年等降水量线与农业类型的关系
4、注意分析:①六月江淮地区阴雨连绵: 受江淮准静止锋的影响
②冬季贵阳阴雨连绵 受昆明准静止锋的影响
③华北地区春旱严重 降水少,太阳高度较大 蒸发旺盛
九月: 夏季风开始南撤
3、我国降水季节和年际变化大的原因
受季风气候的影响 夏季风进退规律的反常
21.[选做题]在A、B、C、D四小题中只能选做两题,每小题10分,共计20分。请在答题卡指定区域内作答,解答时应写出文字说明、证明过程或演算步骤.
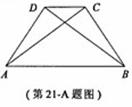 A.选修4 - 1:几何证明选讲
A.选修4 - 1:几何证明选讲
如图,在四边形ABCD中,△ABC≌△BAD.
求证:AB∥CD.
[解析] 本小题主要考查四边形、全等三角形的有关知识,考查推理论证能力。满分10分。
证明:由△ABC≌△BAD得∠ACB=∠BDA,故A、B、C、D四点共圆,从而∠CBA=∠CDB。再由△ABC≌△BAD得∠CAB=∠DBA。因此∠DBA=∠CDB,所以AB∥CD。
B. 选修4 - 2:矩阵与变换
求矩阵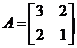 的逆矩阵.
的逆矩阵.
[解析] 本小题主要考查逆矩阵的求法,考查运算求解能力。满分10分。
解:设矩阵A的逆矩阵为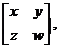 则
则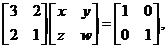
即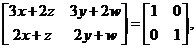 故
故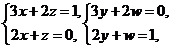
解得: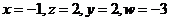 ,
,
从而A的逆矩阵为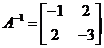 .
.
C. 选修4 - 4:坐标系与参数方程
已知曲线C的参数方程为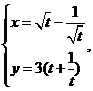 (
(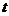 为参数,
为参数,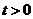 ).
).
求曲线C的普通方程。
[解析] 本小题主要考查参数方程和普通方程的基本知识,考查转化问题的能力。满分10分。
解:因为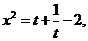 所以
所以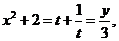
故曲线C的普通方程为: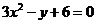 .
.
D. 选修4 - 5:不等式选讲
设 ≥
≥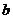 >0,求证:
>0,求证: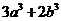 ≥
≥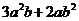 .
.
[解析] 本小题主要考查比较法证明不等式的常见方法,考查代数式的变形能力。满分10分。
证明: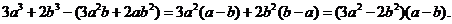
因为 ≥
≥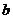 >0,所以
>0,所以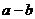 ≥0,
≥0,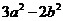 >0,从而
>0,从而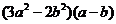 ≥0,
≥0,
即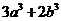 ≥
≥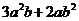 .
.
2009海南宁夏卷
(22)(本小题满分10分)选修4-1;几何证明选讲
 如图,已知
如图,已知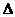 ABC中的两条角平分线
ABC中的两条角平分线 和
和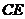 相交于
相交于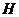 ,
, B=60
B=60 ,
, 在
在 上,且
上,且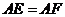 。
。
(1)证明: 四点共圆;
四点共圆;
(2)证明:CE平分 DEF。
DEF。
(22)解:
(Ⅰ)在△ABC中,因为∠B=60°,
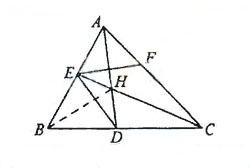 所以∠BAC+∠BCA=120°.
所以∠BAC+∠BCA=120°.
因为AD,CE是角平分线,
所以∠HAC+∠HCA=60°,
故∠AHC=120°.
于是∠EHD=∠AHC=120°.
因为∠EBD+∠EHD=180°,
所以B,D,H,E四点共圆。
(Ⅱ)连结BH,则BH为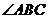 的平分线,得
的平分线,得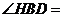 30°
30°
由(Ⅰ)知B,D,H,E四点共圆,
所以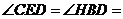 30°
30°
又 60°,由已知可得
60°,由已知可得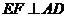 ,
,
可得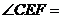 30°
30°
所以CE平分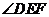
(23)(本小题满分10分)选修4-4:坐标系与参数方程。
已知曲线C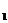 :
: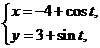 (t为参数), C
(t为参数), C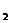 :
: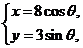 (
( 为参数)。
为参数)。
(1)化C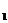 ,C
,C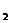 的方程为普通方程,并说明它们分别表示什么曲线;
的方程为普通方程,并说明它们分别表示什么曲线;
(2)若C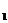 上的点P对应的参数为
上的点P对应的参数为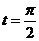 ,Q为C
,Q为C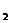 上的动点,求
上的动点,求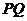 中点
中点 到直线
到直线
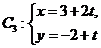 (t为参数)距离的最小值。
(t为参数)距离的最小值。
(23)解:
(Ⅰ)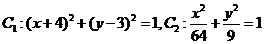
 为圆心是
为圆心是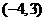 ,半径是1的圆。
,半径是1的圆。
 为中心是坐标原点,焦点在
为中心是坐标原点,焦点在 轴上,长半轴长是8,短半轴长是3的椭圆.
轴上,长半轴长是8,短半轴长是3的椭圆.
(Ⅱ)当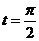 时,
时,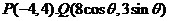 ,故
,故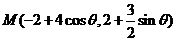
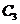 为直线
为直线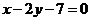 ,
,
M到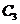 的距离
的距离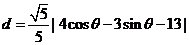
从而当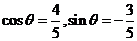 时,
时, 取得最小值
取得最小值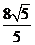
(24)(本小题满分10分)选修4-5:不等式选讲
如图, 为数轴的原点,
为数轴的原点,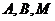 为数轴上三点,
为数轴上三点, 为线段
为线段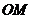 上的动点,设
上的动点,设 表示
表示 与原点的距离,
与原点的距离,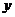 表示
表示 到
到 距离4倍与
距离4倍与 到
到 距离的6倍的和.
距离的6倍的和.
(1)将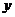 表示为
表示为 的函数;
的函数;
(2)要使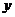 的值不超过70,
的值不超过70, 应该在什么范围内取值?
应该在什么范围内取值?

(24)解:
(Ⅰ)
(Ⅱ)依题意, 满足
满足
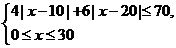
解不等式组,其解集为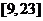
所以
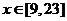
2009辽宁理卷
( 22 ) (本小题满分 10 分)选修 4- l :几何证明选讲
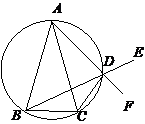 己知△ABC中,AB=AC , D是△ABC外接圆
己知△ABC中,AB=AC , D是△ABC外接圆
劣弧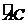 上的点(不与点A , C重合),延长BD至E。
上的点(不与点A , C重合),延长BD至E。
(1)求证:AD 的延长线平分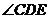 ;
;
(2)若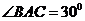 ,△ABC中BC边上的高
,△ABC中BC边上的高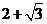 ,
,
求△ABC外接圆的面积.
( 22 ) 解:( 1 )如图,设F为AD延长线上一点,∵A,B,C, D 四点共圆,
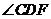 =
=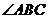 , 又AB=AC ,∴
, 又AB=AC ,∴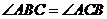 ,且
,且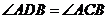 ,
,
∴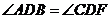 ,对顶角
,对顶角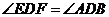 ,故
,故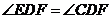 ,
,
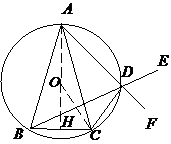 故AD 的延长线平分
故AD 的延长线平分 。
。
.( 2)设O为外接圆圆心,连接AO交BC于H ,则AH⊥BC ,
连接 OC ,由题意 OAC=
OAC= OCA =
OCA =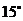 ,
,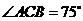 ,
,
∴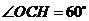 ,设圆半径为r,则
,设圆半径为r,则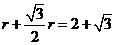 ,
,
得:r= 2 ,故外接圆面积为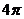 。
。
( 23 ) (本小题满分 10 分)选修 4- 4 :极坐标与参数方程
在直角坐标系xOy中,以O为极点,x轴正半轴为极轴建立极坐标系,曲线C的极坐标方程为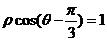 ,M , N分别为曲线C与x轴,y轴的交点.
,M , N分别为曲线C与x轴,y轴的交点.
(1)写出曲线C的直角坐标方程,并求M , N的极坐标;
(2)设M , N的中点为P,求直线OP的极坐标方程.
( 23 )解:(1)由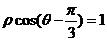 得:
得: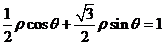 ,
,
∴曲线C的直角坐标方程为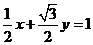 ,即
,即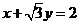 ,
,
当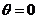 时,
时,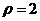 ,∴M的极坐标(2,0);
,∴M的极坐标(2,0);
当 时,
时,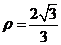 ,∴N的极坐标
,∴N的极坐标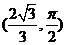 。
。
(2)M的直角坐标为(2,0),N的直角坐标为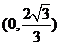 ,∴P的直角坐标为
,∴P的直角坐标为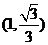 ,
,
则P的极坐标为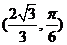 ,直线OP的极坐标方程为
,直线OP的极坐标方程为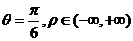 .----10分
.----10分
( 24 ) (本小题满分 10 分)选修 4- 5 :不等式选讲
设函数 ,
,
(1)若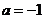 ,解不等式
,解不等式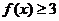 ;
;
(2)如果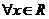 ,
,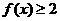 ,求a的取值范围.
,求a的取值范围.
( 24 )解:(1)当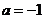 时,
时,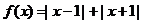 ,由
,由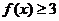 得:
得: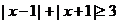 ,
,
(法一)由绝对值的几何意义知不等式的解集为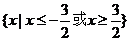 。
。
(法二)不等式可化为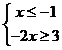 或
或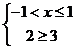 或
或 ,
,
∴不等式的解集为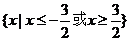 。
。
(2)若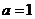 ,
,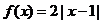 ,不满足题设条件;
,不满足题设条件;
若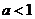 ,
, ,
, 的最小值为
的最小值为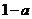 ;
;
若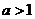 ,
,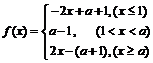 ,
, 的最小值为
的最小值为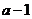 。
。
所以对于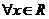 ,
,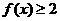 的充要条件是
的充要条件是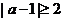 ,从而a的取值范围
,从而a的取值范围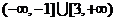 。
。
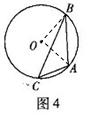
15.(几何证明选讲选做题)如图4,点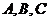 是圆
是圆 上的点, 且
上的点, 且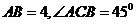 , 则圆
, 则圆 的面积等于
.
的面积等于
.
[解析]解法一:连结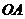 、
、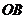 ,则
,则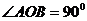 ,∵
,∵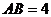 ,
,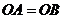 ,∴
,∴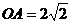 ,则
,则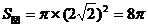 ;解法二:
;解法二: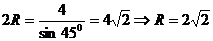 ,则
,则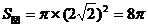 .
.
2009江苏卷
14.(不等式选讲选做题)不等式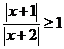 的实数解为 .
的实数解为 .
 [解析]
[解析]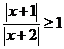
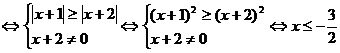 且
且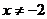 .
.
13.(坐标系与参数方程选做题)若直线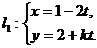 (
(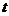 为参数)与直线
为参数)与直线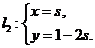 (
(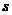 为参数)垂直,则
为参数)垂直,则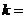 .
.
[解析]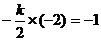 ,得
,得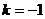 .
.
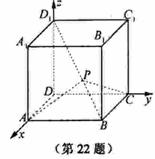
22.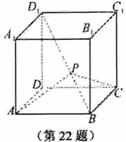 [必做题]如图,设动点P是棱长为1的正方体
[必做题]如图,设动点P是棱长为1的正方体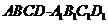 的对角线
的对角线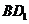 上一点,记
上一点,记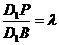 .当
.当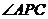 为钝角时,求
为钝角时,求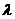 的取值范围.
的取值范围.
解:由题设可知,以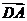 、
、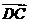 、
、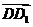 为单位正交基底,建立如图所示的空间直角坐标系
为单位正交基底,建立如图所示的空间直角坐标系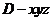 ,
,
则有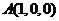 ,
,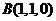 ,
,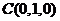 ,
,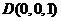
由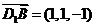 ,得
,得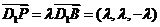 ,
,
所以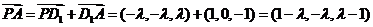
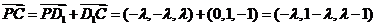
显然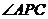 不是平角,所以
不是平角,所以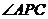 为钝角等价于
为钝角等价于
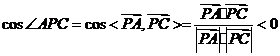 ,则等价于
,则等价于 ,
,
即 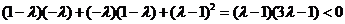 ,得
,得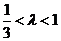 .
.
因此,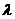 的取值范围是
的取值范围是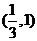
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com