4．一物体从高H处自由下落，当其下落x时，物体的速度恰好是着地时速度的一半，由它下落的位移x=__________。H/4

3．一物体从高处A点自由下落，经B点到达C点，已知B点的速度是C点速度的3/4，BC间距离是7m，则AC间距离是__________m(g取10m/s²)。16

2．小球做自由落体运动，它在前ns内通过的位移与前(n+1)s内通过的位移之比是_____________。n²/(n+1)²

1．某物体从某一较高处自由下落，第1s内的位移是_______m，第2s末的速度是______m/s，前3s 内的平均速度是_________m/s(g取10m/s²)。5,20,15

5．重力加速度的测量

研究自由落体运动通常有两种方法：用打点计时器研究自由落体运动和用频闪摄影法研究自由落体运动。研究的原理和过程与前面对小车运动的研究相同，在对纸带或照片进行数据处理，计算物体运动的加速时，可以有下面两种方法：

(1)图象法求重力加速度

以打点计时器研究自由落体运动为例，对实验得到如图2-4-1所示的纸带进行研究。

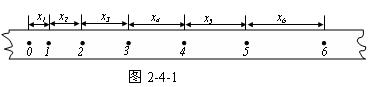
根据匀变速直线运动的一个推论：在一段时间t内的平均速度等于这段时间中间时刻的瞬时速度，有v₁=(x₁+x₂)/2T， v₂=(x₂+x₃)/2T……求出各计数点的瞬时速度后，由加速度的定义：a=Δv/Δt计算出该物体做匀变速直线运动的加速度；或选好计时起点作v-t图象，图象的斜率即为该匀变速直线运动的加速度。

(2)逐差法求重力加速度

图2-4-1中x₁、x₂、x₃、…、x_n是相邻两计数点间的距离,Δx表示两个连续相等的时间里的位移之差,即Δx₁= x₂-x₁, Δx₂= x₃-x₂, ……T是两相邻计数点间的时间间隔且T=0.02n(n为两相邻计数点间的间隔数)。

设物体做匀变速直线运动经过计数点0时的初速度为v₀，加速度为a，由位移公式得： x₁= v₀T+aT²/2，x₂= v₁T+aT²/2，又因为v₁=v₀+aT，所以Δx= x₂-x₁= aT²。因为时间T是个恒量，物体的加速度a也是个恒量，因此，Δx必然是个恒量。这表明，只要物体做匀变速直线运动，它在任意两个连续相等时间里的位移之差就一定相等。

　　 根据x₄-x₁= (x₄-x₃)+ (x₃-x₂)+ (x₂-x₁)=3aT²，可得：

　　 a₁=(x₄-x₁)/3T²，同理可得：a₂=(x₅-x₂)/3T² ；a₃=(x₆-x₃)/3T²。

加速度的平均值为：

a=(a₁+a₂+a₃)/3=[(x₄-x₁)/3T²+(x₅-x₂)/3T²+(x₆-x₃)/3T²]/3

=[( x₄+x₅+x₆)- ( x₁+x₂+x₃)] /9T²

这种计算加速度的方法叫做“逐差法”。

如果不用此法，而用相邻的各x值之差计算加速度再求平均值可得：

a=[(x₂-x₁)/T²+(x₃-x₂)/T²+(x₄-x₃)/T²+(x₅-x₄)/T²+(x₆-x₅)/T²]/5=(x₆-x₁)/5T²

比较可知，逐差法将x₁到x₆各实验数据都利用了，而后一种方法只用上了x₁和x₆两个实验数据，所以失去了多个数据正负偶然误差互相抵消的作用，算出的a值误差较大，因此实验中要采用逐差法。

[范例精析]

例1：甲球的重力是乙球的5倍，甲、乙分别从高H、2H处同时自由落下(H足够大)，下列说法正确的是(　　 )

A．同一时刻甲的速度比乙大

B．下落1m时，甲、乙的速度相同

C．下落过程中甲的加速度大小是乙的5倍

D．在自由下落的全过程，两球平均速度大小相等

　 解析：甲、乙两球同时作初速度为零、加速度为g的直线运动，所以下落过程的任一时刻两者加速度相同、速度相同，但整个过程中的平均速度等于末速度的一半，与下落高度有关。所以正确选项为B。

拓展：自由落体运动是匀加速直线运动的一个特例，其初速度为零、加速度为g，g的大小与重力大小无关。当问题指明(或有明显暗示)空气阻力不能忽略不计时，物体运动就不再是自由落体运动。

例2：水滴由屋檐自由下落，当它通过屋檐下高为1.4m的窗户时，用时0.2s，不计空气阻力，g取10m/s²，求窗台下沿距屋檐的高度。

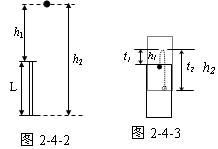
解析：雨滴自由下落，由题意画出雨滴下落运动的示意图如图2-4-2所示,利用自由落体运动的特点和图中的几何关系求解。

如图2-4-2所示h₁=gt²/2……①

h₂=gt²/2……②

t₂=t₁+0.2s……③

h₂=h₁+L……④

由①②③④解得:g(t₁+0.2)²/2=gt₁²/2+L代入数据得t₁=0.6s

所以, h2=g(t₁+0.2)²=10×0.8²/2=3.2m

拓展：由该问题的解题过程可以看出，利用平均速度来解题比较方便、简捷。请思考：本题有无其它解题方法，如有，请验证答案。

例3：升降机以速度v＝4.9m/s匀速竖直上升，升降机内的天花板上有一个螺丝帽突然松脱，脱离天花板。已知升降机天花板到其地板的高度为h＝14.7m。求螺丝帽落到升降机地板所需时间。

解析：解法一：以地面为参照物求解

(1)上升过程：螺丝帽脱离升降机后以v=4.9m/s初速度竖直向上运动

上升到最高点时间：t₁=-v/(-g)=4.9/9.8=0.5s

上升到最高点的位移：h₁=(0-v²)/(-2g)=(0-4.9²)/(-2×9.8)=1.225m

螺丝帽的运动过程如图2-4-3所示，由图中位移约束关系得：

h₁+h=h₂+v(t₁+t₂) 即v²/2g+h=gt₂²/2+v(t₁+t₂)

v²/2g+h=gt₂²/2+v(v/g+t₂)　 代入数据化简得：t₂²+t₂-2.75=0

解得：t₂=1.23 s

因此，螺丝帽落到升降机地板所需时间t=t₁+t₂ =1.73s

解法二：以升降机为参照物求解

我们以升降机为参考系，即在升降机内观察螺丝帽的运动，因为升降机做匀速直线运动，所以相对于升降机而言，螺丝帽的下落加速度仍然是重力加速度。显然，螺丝帽相对于升降机的运动是自由落体运动，相对位移大小即升降机天花板到其地板的高度。由自由落体运动的规律可得

h＝gt²/2

t＝1.73s

拓展：参考系选择不同，不仅物体的运动形式不同，求解时所用的物理规律也可能不同。选择适当的参考系，往往可以使问题的求解过程得到简化。

[能力训练]

4．自由落体运动是匀变速直线运动在v₀=0、a=g时的一个特例,因此其运动规律可由匀变速直线运动的一般规律来推导。

速度公式：v_t=gt

　　 位移公式：h=gt²/2

　　 速度与位移的关系式：v_t²=2gh

在应用自由落体运动的规律解题时，通常选取　　　方向为正方向。

3．　　　　　　　　　　　　　　 叫做自由落体加速度，也叫　　　　　　 　　，通常用符号_____表示。重力加速度g的方向总是_______________；g的大小随地点的不同而略有变化，在地球表面上赤道处重力加速度最小，数值为________，南、北两极处重力加速度_　 ______，数值为_______；g的大小还随高度的变化而变化，高度越大，g值______。但这些差异并不是太大，在通常计算中，地面附近的g取9.8m/s²，在粗略的计算中，g还可以取10m/s²。

2．自由落体运动的特点：物体仅受重力作用；初速度v₀=____，加速度a=____，即初速度为零的匀加速直线运动。

[要点导学]

1．物体只在___________________________________________叫做自由落体运动。这种运动只在没有空气的空间里才能发生，我们所研究的自由落体运动是实际运动的一种抽象，是一种理想化的运动模型：忽略次要因素(空气阻力)、突出主要因素(重力)。生活中的很多落体问题，如果空气阻力的作用比较小，可以忽略，物体的下落也可以近似看作自由落体运动。因此，对生活中的落体运动进行理想化处理是有实际意义的。

10、一矿井深为125m，在井口每隔一定时间自由下落一个小球，当第11个小球刚从井口下落时，第1个小球刚好到达井底。则相邻两个小球开始下落的时间间隔为多少？第3 个小球和第5个小球相隔多少米？