
8..如图,等腰直角△ABC,沿其斜边AB边上的高CD对折,使△ACD与△BCD所在的平面垂直,此时∠ACB等于BA.45° B.60° C.90° D.120°
7. 的值为BA.
的值为BA. D.1
D.1
6. 长方体ABCD-A1B1C1D1中,E、F分别为C1B1,D1B1的中点,且AB=BC,AA1=2AB,则CE与BF所成角的余弦值是DA.
长方体ABCD-A1B1C1D1中,E、F分别为C1B1,D1B1的中点,且AB=BC,AA1=2AB,则CE与BF所成角的余弦值是DA.  B.
B.  C.
C.
 D.
D.

5.数列{an}为等差数列,前n项和为Sn,数列{bn}为等差数列,前n项和为Tn,且 B
B
A.- B.
B.  C.-
C.- D.
D. 
4.(1+x)3+(1+x)4+……+(1+x)50=a0+a1x+a2x2+……+a50x50,则a3= BA. B.
B. C.
C. D.2
D.2
3.足球比赛的计分规则是:胜一场得3分,平一场得1分,负一场得0分,那么一个队打14场共得19分的情况共有BA.3种 B.4种 C.5种 D.6种
2.棱长均为a的三棱锥A-BCD内的一点P到各面的距离之和等于C A. a B.
a B. a C.
a C. D.不能确定
D.不能确定
1.正方体ABCD-A1B1C1D1中,E、F为AA1、AB上的点,若B1E⊥FE,则C1E与EF所成角是C
A.60° B.45°C.90° D.不确定
21.解:设甲预报站预测准确为事件 ,乙预报站预测准确为事件
,乙预报站预测准确为事件 ,
,
1)甲、乙两个天气预报站同时预报准确的概率为:
 ;
;
2)至少有一个预报站预报准确的概率 =
=

3)如果甲站独立预报三次,其中恰有两次预报准确的概率为

 22.1)证明:取
22.1)证明:取 的中点
的中点 ,连
,连 、
、 ,
,
∵ ⊥
⊥ ,
, ⊥
⊥ ,
,
∴ 平面
平面 ,
,
又∵ 、
、 分别是
分别是 、
、 的中点,
的中点,
∴ ∥
∥
∴ ⊥平面
⊥平面 ,∵
,∵
 平面
平面
∴ ⊥
⊥ ,又∵
,又∵ ,且
,且 为
为 的中点,故由平面几 何知识可知
的中点,故由平面几 何知识可知 ,又∵
,又∵ ∥
∥ ,∴
,∴ ∥
∥ ∴
∴ 、
、 、
、 、
、 共面,
共面,
∴ ⊥平面
⊥平面


 ,∴
,∴ ⊥
⊥ .
.
 2)解:作
2)解:作 于
于 ,∵
,∵ 平面
平面 ,∴
,∴ ,∴
,∴ 平面
平面 ,作
,作 于
于 ,连
,连 ,由三垂线定理得
,由三垂线定理得
 ,∴
,∴ 为二面角
为二面角 的一个平面角,
的一个平面角,
在 中,
中, =
=
又∵
 平面
平面 ,∴
,∴


又
 ,∴
,∴ ⊥平面
⊥平面 ,∴
,∴

易得 =
= ,
, =
= . ∴在
. ∴在 中,
中,  =
= ,
,
又在 中,
中, =
= ,
, .
.
23 解:(1)当n=1时,左边=1+1=2= ,右边=
,右边= ,不等式显然成立.
(2)假设n=k时,不等式成立,即
(1+1)(1+(1/4))(1+(1/7))…(1+1/(3k-2))>
,不等式显然成立.
(2)假设n=k时,不等式成立,即
(1+1)(1+(1/4))(1+(1/7))…(1+1/(3k-2))> .?
那么,当n=k+1时,
[(1+1)(1+(1/4))(1+(1/7))…(1+1/(3k-2))](1+1/(3k+1))>
.?
那么,当n=k+1时,
[(1+1)(1+(1/4))(1+(1/7))…(1+1/(3k-2))](1+1/(3k+1))> (1+1/(3k+1))=
(1+1/(3k+1))= ·(3k+2)/(3k+1).
?∵ (
·(3k+2)/(3k+1).
?∵ ( ·(3k+2)/(2k+1))3-(
·(3k+2)/(2k+1))3-(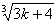 )3=((3k+2)3/(3k+1)2)-(3k+4)=((3k+2)3-(3k+1)2(3k+4)/(3k+1)2)=(9k+4)/(3k+1)2)>0,
∴
)3=((3k+2)3/(3k+1)2)-(3k+4)=((3k+2)3-(3k+1)2(3k+4)/(3k+1)2)=(9k+4)/(3k+1)2)>0,
∴  ·(3k+2)/(3k+1)>
·(3k+2)/(3k+1)>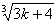 =
= .
? ∴ 当n=k+1时,不等式亦成立.
由(1)、(2)证明知,不等式对一切n∈N都成立.
说明:在第二步证明
.
? ∴ 当n=k+1时,不等式亦成立.
由(1)、(2)证明知,不等式对一切n∈N都成立.
说明:在第二步证明 ·(3k+2)/(3k+1)>
·(3k+2)/(3k+1)> 时,我们还用到了比较法.
时,我们还用到了比较法.
20.(1)取一次就能安装的概率为 取二次就能安装的概率:
取二次就能安装的概率:
最多取2次零件就能安装的概率为
(2)由于随机变量ξ表示取得合格品前已取出的次品数,所以可能的取值为0、1、2;
 ∴ξ的分布列为
∴ξ的分布列为
|
ξ |
0 |
1 |
2 |
|
P |
 |
 |
 |
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com