
2. abortion. n. ①[u]人工流产,打胎 ②[c] 人工流产手术 ③[c]完全失败的计划或行动
1. abolish. vt 废除,废 止(习俗、制度)
eg: Should we abolish the death penalty?我们应该废除死刑吗?
2.已知函数 ,
, .求
.求 的单调区间和值域.
的单调区间和值域.
1.已知a为实数,
(1)求导数 ;(2)若
;(2)若 ,求
,求 在[-2,2] 上的最大值和最小值.
在[-2,2] 上的最大值和最小值.
4.函数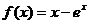 在
在 上的最大值是________;最小值是_______.
上的最大值是________;最小值是_______.
归纳反思:
合作探究:
3.已知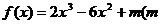 为常数)在[-2,2]上有最大值3,那么此函数在[-2,2]上的最小值为
.
为常数)在[-2,2]上有最大值3,那么此函数在[-2,2]上的最小值为
.
2.函数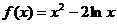 的最小值是( )
的最小值是( )
A 0 B -1 C 1 D 2
1.函数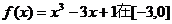 上的最大值,最小值分别是( )
上的最大值,最小值分别是( )
A.1,-1 B.1,-17 C.3,-17 D.9,-19
1.3.2利用导数研究函数的极值
(第二课时)
|
学习目标: ⒈理解函数的最大值和最小值的概念,掌握可导函数  在闭区间 在闭区间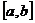 上所有点(包括端点 上所有点(包括端点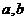 )处的函数中的最大(或最小)值必有的充分条件; )处的函数中的最大(或最小)值必有的充分条件;⒉掌握用导数求函数的极值及最值的方法和步骤 学习重点难点: 利用导数求函数的最大值和最小值的方法. 自主学习 一、知识再现: 求可导函数f(x)的极值的步骤: (1)确定函数的定义区间,求导数f′(x)  (2)求方程f′(x)=0的根  (3)用函数的导数为0的点,顺次将函数的定义区间分成若干小开区间,并列成表格.检查f′(x)在方程根左右的值的符号,如果左正右负,那么f(x)在这个根处取得极大值;如果左负右正,那么f(x)在这个根处取得极小值;如果左右不改变符号,那么f(x)在这个根处无极值  二、新课探究 1、函数的最大值和最小值 观察图中一个定义在闭 区间 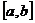 上的函数 上的函数 的 的图象.图中 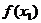 与 与 是 是极小值,  是极大值.函 是极大值.函数  在 在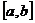 上的最大值 上的最大值 是 是 ,最小值是 ,最小值是 . .一般地,在闭区间 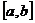 上连续的函数 上连续的函数 在 在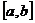 上必有最大值 上必有最大值与最小值. 说明:⑴在开区间 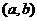 内连续的函数 内连续的函数 不一定有最大值与最小值.如函数 不一定有最大值与最小值.如函数 在 在 内连续,但没有最大值与最小值; 内连续,但没有最大值与最小值;⑵函数的最值是比较整个定义域内的函数值得出的;函数的极值是比较极值点附近函数值得出的. ⑶函数  在闭区间 在闭区间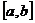 上连续,是 上连续,是 在闭区间 在闭区间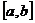 上有最大值与最小值的充分条件而非必要条件. 上有最大值与最小值的充分条件而非必要条件.(4)函数在其定义区间上的最大值、最小值最多各有一个,而函数的极值可能不止一个,也可能没有一个  2、利用导数求函数的最值步骤: 由上面函数  的图象可以看出,只要把连续函数所有的极值与定义区间端点的函数值进行比较,就可以得出函数的最值了. 的图象可以看出,只要把连续函数所有的极值与定义区间端点的函数值进行比较,就可以得出函数的最值了.设函数  在 在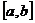 上连续,在 上连续,在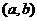 内可导,则求 内可导,则求 在 在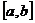 上的最大值与最小值的步骤如下: 上的最大值与最小值的步骤如下:⑴求  在 在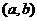 内的极值; 内的极值;⑵将  的各极值与 的各极值与 、 、 比较得出函数 比较得出函数 在 在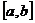 上的最值 上的最值 三、例题解析: 例1求函数  在区间 在区间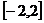 上的最大值与最小值 上的最大值与最小值 解:先求导数,得 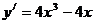 令  =0即 =0即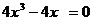 解得 解得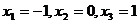 导数  的正负以及 的正负以及 , , 如下表 如下表
从上表知,当 值4 例2
已知
函数,在[1,+∞)上是增函数;(2) 出 解:设g(x)= 在[1,+∞)上是增函数 ∴g(x)在(0,1)上是减函数,在[1,+∞)上是增函数. ∴ 经检验,a=1,b=1时,f(x)满足题设的两个条件. 课堂巩固: 26.[广东省实验中学2008学年高三第二次阶段测试试卷数学(理科)第15题](13分) 在锐角△ABC中, (Ⅰ)求B的值; (Ⅱ)求 同步练习册答案 湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区 违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com版权声明:本站所有文章,图片来源于网络,著作权及版权归原作者所有,转载无意侵犯版权,如有侵权,请作者速来函告知,我们将尽快处理,联系qq:3310059649。 ICP备案序号: 沪ICP备07509807号-10 鄂公网安备42018502000812号 |