已知函数其中a>0.

（I）求函数f(x)的单调区间；

（II）若函数f（x）在区间（-2，0）内恰有两个零点，求a的取值范围；

（III）当a=1时，设函数f（x）在区间[t,t+3]上的最大值为M（t），最小值为m（t）,记g(t)=M(t)-m(t),求函数g(t)在区间[-3，-1]上的最小值。

【考点定位】本小题主要考查导数的运算，利用导数研究函数的单调性、函数的零点，函数的最值等基础知识.考查函数思想、分类讨论思想.考查综合分析和解决问题的能力.

已知函数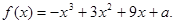

（Ⅰ）求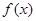的单调减区间；

（Ⅱ）若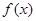在区间[－2，2].上的最大值为20，求它在该区间上的最小值.

【解析】(1)求导令导数小于零.

(2)利用导数列表求极值，最值即可.

函数f(x)=(2x+3)²的导数f′(x)=            。

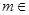已知R，函数．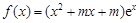

⑴若函数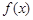没有零点，求实数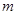的取值范围；

⑵若函数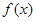存在极大值，并记为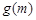，求的表达式；

⑶当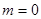时，求证：．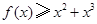

【解析】(1)求导研究函数f(x)的最值，说明函数f(x)的最大值<0,或f(x)的最小值>0.

(2)根据第（1）问的求解过程，直接得到g(m).

（3）构造函数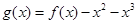,证明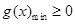即可，然后利用导数求g(x)的最小值.