阅读下列材料,并解决后面的问题.
★阅读材料:
我国是历史上较早发现并运用“勾股定理”的国家之一.我中古代把直角三角形中较短的直角边称为“勾”,较长的直角边称为“股”,斜边称为“弦”,“勾股定理”因此而得名.
勾股定理:如果直角三角形两直角边长分别为a,b,斜边长为c,那么a
2+b
2=c
2.即直角三角形两直角边的平方和等于斜边的平方.请运用“勾股定理”解决以下问题:
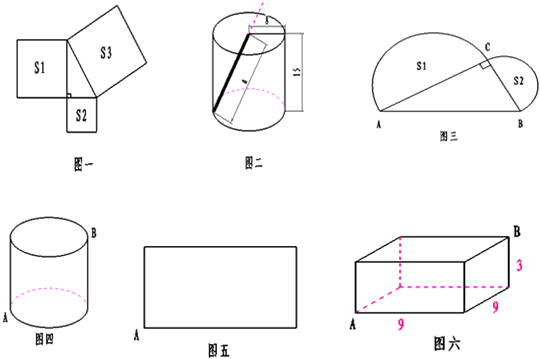
(1)如图一,分别以直角三角形的边为边长作正方形,其中s
1=400,s
2=225,则s
3=
625
625
.
(2)如图二,是一个园柱形饮料罐,底面半径=8,高=15,顶面正中有一个小园孔,则一条直达底部的直吸管的最大长度是
17
17
.注:罐壁厚度和顶部园孔直径忽略不计.
(3)如图三,所示的直角三角形中,AB=6.则s
1+s
2的值=
13.5
13.5
. 注π值取3.
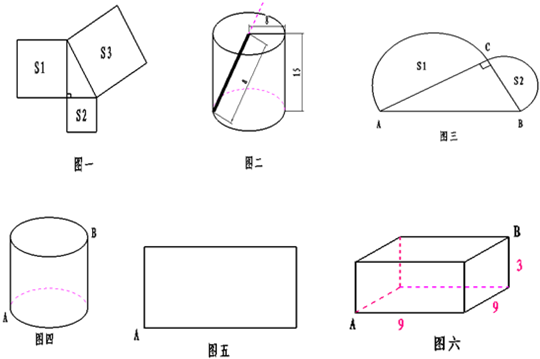
(4)如图四的圆柱,高=5厘米,底面半径=4厘米,在园柱底面A点有一只蚂蚁,它想吃到与A点相对的B点处的食物,需要爬行的路程是多少?小聪是这样思考的:
①将该园柱的侧面展开后得到一个长方形,如图五所示(A点的位置已经给出),请在图中中标出B点的位置并连接AB.
②小聪认为线段AB的长度是蚂蚁爬行的最短路程,那么蚂蚁爬行的最短路程是
13
13
厘米.注:π值取3.
(5)如图六,在长方形的底面A点有一只蚂蚁,想吃到上底面与A点相对的B点处的食物,它沿长方形表面爬行的最短路程是
15
15
厘米.


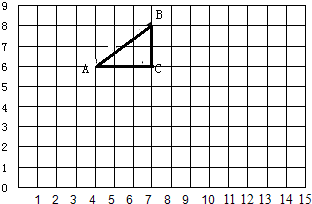

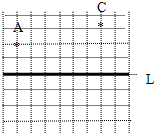 (1)以L为对称轴画出A点的对称点A′,连接A′C使A′C和直线L相交于为O点,连接AO,量出“AO+OC”的距离和为
(1)以L为对称轴画出A点的对称点A′,连接A′C使A′C和直线L相交于为O点,连接AO,量出“AO+OC”的距离和为