
| 图中所示,点A、O、D以及B、O、C分别在一条直线上,则圆中弦的条数为 |
|
A. 2 B. 3 C. 4 D. 5 |
科目:初中数学 来源:素质教育新学案·初中几何·第三册 题型:013
如图所示,点A、O、D以及B、O、C分别在一条直线上,则圆中弦的条数为
[ ]

A.2 B.3 C.4 D.5
科目:初中数学 来源: 题型:044
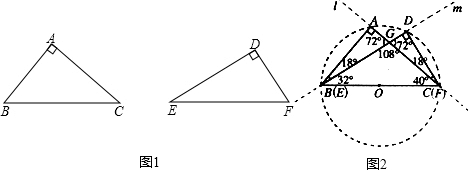
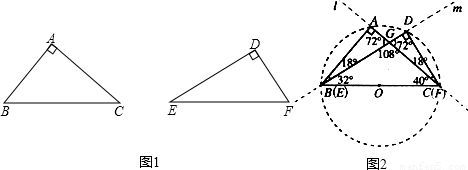
如图1所示,一张三角形纸片ABC,∠ACB=90°,AC=8,BC=6.沿斜边AB的中线CD把这张纸片剪成![]() 和
和![]() 两个三角形(如图2所示).将纸片
两个三角形(如图2所示).将纸片![]() 沿直线
沿直线![]() (AB)方向平移(点
(AB)方向平移(点![]() 始终在同一直线上),当点
始终在同一直线上),当点![]() 于点B重合时,停止平移.在平移过程中,
于点B重合时,停止平移.在平移过程中,![]() 与
与![]() 交于点E,
交于点E,![]() 与
与![]() 分别交于点F、P.
分别交于点F、P.
(1) 当![]() 平移到如图3所示的位置时,猜想图中的
平移到如图3所示的位置时,猜想图中的![]() 与
与![]() 的数量关系,并证明你的猜想;
的数量关系,并证明你的猜想;
(2)
设平移距离(3)
对于(2)中的结论是否存在这样的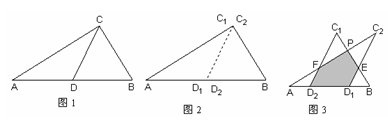
科目:初中数学 来源:单科王牌 九年级数学(上) 题型:044
如图所示,矩形ABCD中,AB=10cm,BC=20cm,P、Q两点同时从A点出发.分别以1厘米/秒和2厘米/秒的速度沿A→B→C→D→A运动,当Q点回到A点时,P、Q两点即停止运动,设P、Q运动时间为t秒.
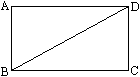
(1)当P、Q分别在AB边和BC边上运动时,设以P、B、Q为顶点的三角形面积为S.请写出S关于t的函数解析式及自变量t的取值范围;
(2)在整个运动过程中,t取何值时,PQ与BD垂直.
科目:初中数学 来源: 题型:022
如图所示,等边△ABC放置在平面直角坐标系中,则A点坐标是________,B点坐标是________,C点坐标是________.
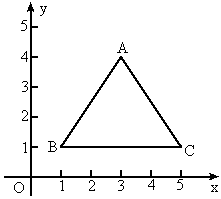
(1)若将各点的横坐标分别减去2,纵坐标保持不变,则所得各点的坐标分别为 ________,
________,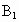 ________,
________, ;将各点用线段依次结起来,所得
;将各点用线段依次结起来,所得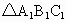 与原△ABC相比________不变,△ABC向________2个单位长度.
与原△ABC相比________不变,△ABC向________2个单位长度.
(2)若将各点的纵坐标分别加上3,横坐标保持不变,则所得各点的坐标分别为 ________,
________,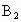 ________,
________, ;将各点用线段依次结起来,所得
;将各点用线段依次结起来,所得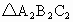 与原△ABC相比________不变,△ABC向________3个单位长度.
与原△ABC相比________不变,△ABC向________3个单位长度.
(3)若将各点的横坐标分别变为它的相反数,纵坐标保持不变,则所得各点的坐标分别为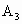 ________,
________,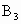 ________,
________, ;将各点用线段依次结起来,所得
;将各点用线段依次结起来,所得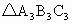 与原△ABC关于________轴对称.
与原△ABC关于________轴对称.
(4)若将A点的坐标乘以2,A点的横坐标及B、C两点坐标不变,则所得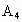 点坐标为
点坐标为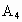 ________,将各点用线段依次连结起来,所得
________,将各点用线段依次连结起来,所得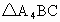 的形状为________.
的形状为________.
(5)若将△ABC以x轴为对称轴翻折得到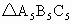 ,则所得各点坐标分别为
,则所得各点坐标分别为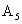 ________;
________;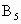 ________;
________;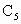 ________;此时各点的横坐标与原△ABC各对应点的横坐标________,纵坐标________.
________;此时各点的横坐标与原△ABC各对应点的横坐标________,纵坐标________.
科目:初中数学 来源: 题型:
科目:初中数学 来源: 题型:解答题
科目:初中数学 来源:2005-2006学年北京市海淀区上地实验中学九年级(上)期末数学试卷(解析版) 题型:解答题
科目:初中数学 来源:2005-2006学年北京市海淀区九年级(上)期末数学试卷(解析版) 题型:解答题
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com