
| 在平面直角坐标系中,将五边形的各顶点的横坐标都减5,纵坐标保持不变,那么该五边形 |
A.横向向右平移5个单位 B.横向向左平移5个单位 C.纵向向上平移5个单位 D.纵向向下平移5个单位 |
科目:初中数学 来源:竞赛题 题型:单选题
科目:初中数学 来源: 题型:
 在平面直角坐标系中(每个小方格的边长为单位1)描出下列各点,并将各点用线段依次连接起来:A(0,2),B(-1,-2),C(2,0),D(-2,0),E(1,-2),A(0,2);观察得到的图形,你觉得它的形状象
在平面直角坐标系中(每个小方格的边长为单位1)描出下列各点,并将各点用线段依次连接起来:A(0,2),B(-1,-2),C(2,0),D(-2,0),E(1,-2),A(0,2);观察得到的图形,你觉得它的形状象科目:初中数学 来源:同步题 题型:探究题
科目:初中数学 来源:学习周报 数学 沪科九年级版 2009-2010学年 第5期 总第161期 沪科版 题型:022
在平面直角坐标系中描出点
A(4,2)、B(2,4)、C(0,4)、D(0,2)、E(2,0),顺次连接点A、B、C、D、E、A得到一个五边形ABCDE.将点A、B、C、D、E的横坐标和纵坐标都除以2,得到另外五个点A1、B1、C1、D1、E1,顺次连接A1、B1、C1、D1、E1、A1,得到一个新的五边形A1B1C1D1E1,那么五边形A1B1C1D1E1与五边形ABCDE的形状________;五边形A1B1C1D1E1可以看成将五边形ABCDE缩小到原来的________得到的.科目:初中数学 来源: 题型:044
(1)在平面直角坐标系中描出点A(4,2),B(2,4),C(0,4),D(0,2);E(2,0),顺次连接点A,B,C,D,E,A,得到一个五边形ABCDE.
(2)将点A,B,C,D,E的横坐标和纵坐标都除以2,得到五个新的点,顺次连接这五个点,得到一个新的五边形.这两个五边形相似吗?如果将点A,B,C,D,E的横坐标和纵坐标都乘以3呢?
科目:初中数学 来源: 题型:
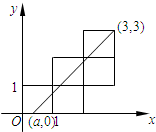 五个边长为1的正方形如图摆放在平面直角坐标系中,经过(a,0),(3,3)的一条直线将这五个正方形分成面积相等的两部分,则a的值是( )
五个边长为1的正方形如图摆放在平面直角坐标系中,经过(a,0),(3,3)的一条直线将这五个正方形分成面积相等的两部分,则a的值是( )A、
| ||
B、
| ||
C、
| ||
D、
|
科目:初中数学 来源: 题型:单选题
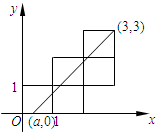 五个边长为1的正方形如图摆放在平面直角坐标系中,经过(a,0),(3,3)的一条直线将这五个正方形分成面积相等的两部分,则a的值是
五个边长为1的正方形如图摆放在平面直角坐标系中,经过(a,0),(3,3)的一条直线将这五个正方形分成面积相等的两部分,则a的值是



科目:初中数学 来源:2013年初中毕业升学考试(辽宁锦州卷)数学(解析版) 题型:解答题
如图,抛物线 经过△ABC的三个顶点,点A坐标为(0,3),点B坐标为(2,3),点C在x轴的正半轴上.
经过△ABC的三个顶点,点A坐标为(0,3),点B坐标为(2,3),点C在x轴的正半轴上.
(1)求该抛物线的函数关系表达式及点C的坐标;
(2)点E为线段OC上一动点,以OE为边在第一象限内作正方形OEFG,当正方形的顶点F恰好落在线段AC上时,求线段OE的长;
(3)将(2)中的正方形OEFG沿OC向右平移,记平移中的正方形OEFG为正方形DEFG,当点E和点C重合时停止运动.设平移的距离为t,正方形DEFG的边EF与AC交于点M,DG所在的直线与AC交于点N,连接DM,是否存在这样的t,使△DMN是等腰三角形?若存在,求出t的值;若不存在,请说明理由;
(4)在上述平移过程中,当正方形DEFG与△ABC的重叠部分为五边形时,请直接写出重叠部分的面积S与平移距离t的函数关系式及自变量t的取值范围;并求出当t为何值时,S有最大值,最大值是多少?

科目:初中数学 来源: 题型:解答题
如图,抛物线 经过△ABC的三个顶点,点A坐标为(0,3),点B坐标为(2,3),点C在x轴的正半轴上.
经过△ABC的三个顶点,点A坐标为(0,3),点B坐标为(2,3),点C在x轴的正半轴上.
(1)求该抛物线的函数关系表达式及点C的坐标;
(2)点E为线段OC上一动点,以OE为边在第一象限内作正方形OEFG,当正方形的顶点F恰好落在线段AC上时,求线段OE的长;
(3)将(2)中的正方形OEFG沿OC向右平移,记平移中的正方形OEFG为正方形DEFG,当点E和点C重合时停止运动.设平移的距离为t,正方形DEFG的边EF与AC交于点M,DG所在的直线与AC交于点N,连接DM,是否存在这样的t,使△DMN是等腰三角形?若存在,求出t的值;若不存在,请说明理由;
(4)在上述平移过程中,当正方形DEFG与△ABC的重叠部分为五边形时,请直接写出重叠部分的面积S与平移距离t的函数关系式及自变量t的取值范围;并求出当t为何值时,S有最大值,最大值是多少?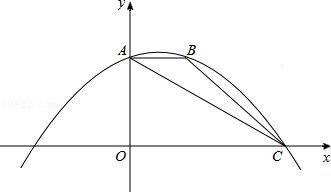
科目:初中数学 来源:不详 题型:解答题
 经过△ABC的三个顶点,点A坐标为(0,3),点B坐标为(2,3),点C在x轴的正半轴上.
经过△ABC的三个顶点,点A坐标为(0,3),点B坐标为(2,3),点C在x轴的正半轴上.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com