
| 如图,E、F分别是正方形ABCD的边CD、AD上的点,且CE=DF,AE、BF相交于点O,下列结论 ①AE=BF;②AE⊥BF;③AO=OE;④  中,错误的有 中,错误的有 |
|
A.1个 B.2个 C.3个 D.4个 |
科目:初中数学 来源:解题升级 解题快速反应一典通 九年级级数学 题型:044
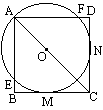
如图,已知O是正方形ABCD对角线AC上一点,以O为圆心,OA的长为半径的圆O与BC相切于M,与AB、AD分别相交于E、F.(1)求证:CD与⊙O相切;(2)若正方形ABCD的边长为1,求⊙O的半径:(3)对于以点M、E、A、F以及CD与⊙O的切点N为顶点五边形的五条边,从相等关系考虑,你可以得出什么结论?请给出证明.
科目:初中数学 来源: 题型:
科目:初中数学 来源:江苏省盐城市解放路学校2012届九年级下学期阶段性测试数学试题 题型:044
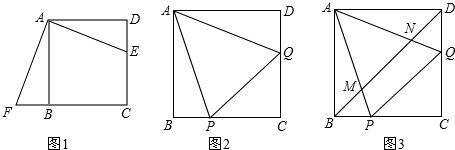
正方形ABCD中,E是CD边上一点.
(1)将△ADE绕点A按顺时针方向旋转,使AD、AB重合,得到△ABF,如图所示.观察可知:与DE相等的线段是________,∠AFB=∠________.
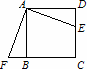
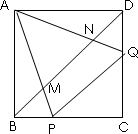
(2)如图,正方形ABCD中,P、Q分别是BC、CD边上的点,且∠PAQ=45°,试通过旋转的方式说明:DQ+BP=PQ
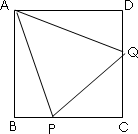
(3)在(2)题中,连接BD分别交AP、AQ于M、N,你还能用旋转的思想说明 BM2+DN2=MN2
科目:初中数学 来源: 题型:
| 1 | 4 |
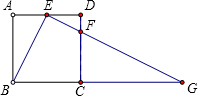 接EF并延长交BC的延长线于点G.
接EF并延长交BC的延长线于点G.科目:初中数学 来源: 题型:
科目:初中数学 来源: 题型:
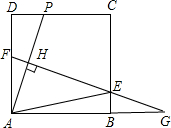 如图,己知正方形ABCD的边长为12,点P为CD边上的一个动点(点P与D、C不重合),AP的垂直平分线EF分别交AD、AP、BC于点F、H、E,交AB的延长线于点G.
如图,己知正方形ABCD的边长为12,点P为CD边上的一个动点(点P与D、C不重合),AP的垂直平分线EF分别交AD、AP、BC于点F、H、E,交AB的延长线于点G.科目:初中数学 来源: 题型:
 20、如图,点E、F分别是正方形ABCD的边CD、AD上的点,且CE=DF,AE、BF相交于点O,下面四个结论:(1)AE=BF,(2)AE⊥BF,(3)AO=OE,(4)S△AOB=S四边形DEOF,其中正确结论的序号是
20、如图,点E、F分别是正方形ABCD的边CD、AD上的点,且CE=DF,AE、BF相交于点O,下面四个结论:(1)AE=BF,(2)AE⊥BF,(3)AO=OE,(4)S△AOB=S四边形DEOF,其中正确结论的序号是科目:初中数学 来源: 题型:
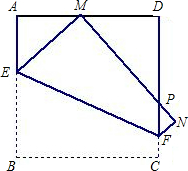 落在AD边上的点M处,点C落在点N处,MN与CD交于点P.
落在AD边上的点M处,点C落在点N处,MN与CD交于点P.科目:初中数学 来源:2012年初中毕业升学考试(四川绵阳卷)数学(带解析) 题型:解答题
如图,正方形ABCD中,E、F分别是边AD、CD上的点,DE=CF,AF与BE相交于O,DG⊥AF,垂足为G。
(1)求证:AF⊥BE;
(2)试探究线段AO、BO、GO的长度之间的数量关系;
(3)若GO:CF=4:5,试确定E点的位置。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com