科目：初中数学 来源： 题型：

查看答案和解析>>

科目：初中数学 来源： 题型：

查看答案和解析>>

科目：初中数学 来源：不详 题型：单选题

查看答案和解析>>

科目：初中数学 来源： 题型：

如图，已知等边△ABC中，D为AC上一动点．CD=nAD，连接BD，M为线段BD上一点，∠AMD=60°，AM交BC于E．
（1）若n=1，如图1，则

BE

CE

=

1

1

，

BM

DM

=

2

2

；
（2）若n=2，如图2，求证：2AB=3BE；
（3）当

BE

AB

=

7

9

时，则n的值为

3.5

3.5

．

查看答案和解析>>

科目：初中数学 来源：期中题 题型：单选题

查看答案和解析>>

科目：初中数学 来源： 题型：阅读理解

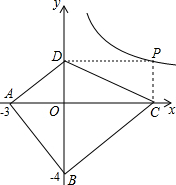阅读理解：
对于任意正实数a、b，∵(

a

-

b

)2≥0，∴a-2

ab

+b≥0，
∴a+b≥2

ab

，只有当a=b时，等号成立．
结论：在a+b≥2

ab

（a、b均为正实数）中，若ab为定值p，则a+b≥2

p

，只有当a=b时，a+b有最小值2

p

．
（1）根据上述内容，回答下列问题：
若m＞0，只有当m=

1

1

时，m+

1

m

有最小值

2

2

．
（2）探索应用：如图，已知A（-3，0），B（0，-4），P为双曲线y=

12

x

（x＞0）图象上的任意一点，过点P作PC⊥x轴于点C，PD⊥y轴于点D．求四边形ABCD面积的最小值．
（3）判断此时四边形ABCD的形状，说明理由．

查看答案和解析>>

科目：初中数学 来源： 题型：

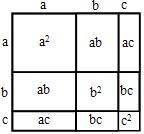27、如图，已知大正方形的边长为a+b+c，利用图形的面积关系可得：（a+b+c）²=a²+b²+c²+2ab+2bc+2ac．当大正方形的边长为a+b+c+d时，利用图形的面积关系可得：（a+b+c+d）²=a²+b²+c²+d²+2ab+2ac+2ad+2bc+2bd+2cd．一般地，n个数的和的平方等于这n个数的平方和加上它们两两乘积的2倍．
根据以上结论解决下列问题：
（1）若a+b+c=6，a²+b²+c²=14，则ab+bc+ac=

11

；
（2）从-4，-2，-1，3，5这五个数中任取两个数相乘，再把所有的积相加，若和为m，求m的值．

查看答案和解析>>

科目：初中数学 来源： 题型：阅读理解

阅读理解：对于任意正实数a，b，（

a

-

b

）²≥0，∴a-2

ab

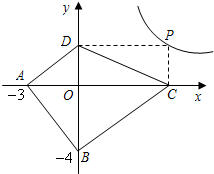+b≥0，只有当a=b时，等号成立．
结论：在a+b≥2

ab

（a，b均为正实数）中，若ab为定值p，则a+b≥2

p

，
只有当a=b时，a+b有最小值2

p

．
根据上述内容，回答下列问题：
（1）若m＞0，只有当m=

1

1

时，m+

1

m

有最小值

2

2

；
（2）探索应用：已知A（-3，0），B（0，-4），点P为双曲线y=

12

x

(x＞0)上的任意一点，过点P作PC⊥x轴于点C，PD⊥y轴于D．求四边形ABCD面积的最小值，并说明此时四边形ABCD的形状．

查看答案和解析>>