练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    函数的值域为，则它的定义域可以是

    A.
    B.
    C.
    D.
    A
    请在这里输入关键词：
    相关习题

    科目：高中数学 来源：2010-2011学年河北省高三期中考试理科数学卷 题型：选择题

    函数的值域为，则它的定义域可以是         （    ）

    A．              B．          C．         D．

     

    查看答案和解析>>

    科目：高中数学 来源：0103 期中题 题型：单选题

    函数的值域为，则它的定义域可以是
    [     ]
    A.
    B.
    C.
    D.

    查看答案和解析>>

    科目：高中数学 来源：不详 题型：单选题

    函数的值域为，则它的定义域可以是  （   ）
    A．B．C．D．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    一个函数f（x），如果对任意一个三角形，只要它的三边长a，b，c都在f（x）的定义域内，就有f（a），f（b），f（c）也是某个三角形的三边长，则称f（x）为“保三角形函数”．
    （Ⅰ）判断f1(x)=
    		x
    ，f2（x）=x，f3（x）=x2中，哪些是“保三角形函数”，哪些不是，并说明理由；
    （Ⅱ）如果g（x）是定义在R上的周期函数，且值域为（0，+∞），证明g（x）不是“保三角形函数”；
    （Ⅲ）若函数F（x）=sinx，x∈（0，A）是“保三角形函数”，求A的最大值．
    （可以利用公式sinx+siny=2sin
    x+y
    2
    cos
    x-y
    2
    ）

    查看答案和解析>>

    科目：高中数学 来源：成功之路·突破重点线·数学（学生用书） 题型：044

    下面的命题正确的有哪些？

    (1)函数y＝f－1(x)的反函数是y＝f(x)；

    (2)如果点M(a，b)在函数y＝f(x)的图象上，且反函数存在，则点(b，a)一定在它的反函数的图象上；

    (3)关于直线y＝x对称的两个图形一定是互为反函数的一对函数的图象；

    (4)因为y＝f(x)的图象与y＝f－1(x)的图象关于y＝x对称，所以y＝f(x)的图象与y＝f－1(x)的图象不可能相交；

    (5)如果y＝f(x)存在反函数，那么f－1(x)的定义域一定是f(x)的值域；

    (6)y＝f(x)在[a，b]上是增函数，那么f－1(x)在[a，b]上也是增函数．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    (08年海淀区期中练习理)（14分）

    一个函数，如果对任意一个三角形，只要它的三边长都在的定义域内，就有也是某个三角形的三边长，则称为“保三角形函数”．

    （I）判断，，中，哪些是“保三角形函数”，哪些不是，并说明理由；

    （II）如果是定义在上的周期函数，且值域为，证明不是“保三角形函数”；

    （III）若函数，是“保三角形函数”，求的最大值．

    （可以利用公式）

    查看答案和解析>>

    科目：高中数学 来源：2008-2009学年上海市八校高三（上）第一次联考数学试卷（文理合卷）（解析版） 题型：解答题

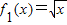    一个函数f（x），如果对任意一个三角形，只要它的三边长a，b，c都在f（x）的定义域内，就有f（a），f（b），f（c）也是某个三角形的三边长，则称f（x）为“保三角形函数”．
    （Ⅰ）判断，f2（x）=x，f3（x）=x2中，哪些是“保三角形函数”，哪些不是，并说明理由；
    （Ⅱ）如果g（x）是定义在R上的周期函数，且值域为（0，+∞），证明g（x）不是“保三角形函数”；
    （Ⅲ）若函数F（x）=sinx，x∈（0，A）是“保三角形函数”，求A的最大值．
    （可以利用公式）

    查看答案和解析>>

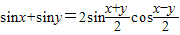    科目：高中数学 来源：2009年高考数学压轴试卷集锦（2）（解析版） 题型：解答题

    一个函数f（x），如果对任意一个三角形，只要它的三边长a，b，c都在f（x）的定义域内，就有f（a），f（b），f（c）也是某个三角形的三边长，则称f（x）为“保三角形函数”．
    （Ⅰ）判断，f2（x）=x，f3（x）=x2中，哪些是“保三角形函数”，哪些不是，并说明理由；
    （Ⅱ）如果g（x）是定义在R上的周期函数，且值域为（0，+∞），证明g（x）不是“保三角形函数”；
    （Ⅲ）若函数F（x）=sinx，x∈（0，A）是“保三角形函数”，求A的最大值．
    （可以利用公式）

    查看答案和解析>>

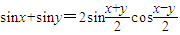    科目：高中数学 来源：2008年北京市海淀区高考数学一模试卷（理科）（解析版） 题型：解答题

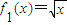    一个函数f（x），如果对任意一个三角形，只要它的三边长a，b，c都在f（x）的定义域内，就有f（a），f（b），f（c）也是某个三角形的三边长，则称f（x）为“保三角形函数”．
    （Ⅰ）判断，f2（x）=x，f3（x）=x2中，哪些是“保三角形函数”，哪些不是，并说明理由；
    （Ⅱ）如果g（x）是定义在R上的周期函数，且值域为（0，+∞），证明g（x）不是“保三角形函数”；
    （Ⅲ）若函数F（x）=sinx，x∈（0，A）是“保三角形函数”，求A的最大值．
    （可以利用公式）

    查看答案和解析>>


    同步练习册答案