练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    a为1-b和1+b的等比中项，ab的最大值为

    A、
    B、
    C、2
    D、4
    A
    请在这里输入关键词：
    相关习题

    科目：高中数学 来源：0108 期中题 题型：单选题

    a为1-b和1+b的等比中项，ab的最大值为
    [     ]
    A、
    B、
    C、2
    D、4
    ≌

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    给出下列四个命题,其中不正确的命题的序号是________________.

    ①若数列{an}的奇数项为2-，偶数项为（2+）-1，则此数列既是等差数列又是等比数列  ②若数列{an}的前n项和Sn=an-1(a为非零常数)，则{an}可以是等差数列，也可以是等比数列  ③若a,b,c是等差数列{an}的第p,q,r项，同时又是等比数列{bn}的第p,q,r项，则ab-c·bc-a·ca-b=1  ④若sin2x和sinx分别是sinθ和cosθ的等差中项和等比中项，则cos2x=

    查看答案和解析>>

    科目：高中数学 来源：奉贤区一模 题型：解答题

    已知：函数f(x)=
    x
    ax+b
    (a，b∈R，ab≠0)    ，f(2)=
    2
    3
    ，f(x)=x    有唯一的根．
    （1）求a，b的值；
    （2）数列{an}对n≥2，n∈N总有an=f（an-1），a1=1；求证{
    1
    an
    }    为等差数列，并求出{an}的通项公式．
    （3）是否存在这样的数列{bn}满足：{bn}为{an}的子数列（即{bn}中的每一项都是{an}的项）且{bn}为无穷等比数列，它的各项和为
    1
    2
    ．若存在，找出一个符合条件的数列{bn}，写出它的通项公式；若不存在，说明理由．

    查看答案和解析>>

    科目：高中数学 来源：奉贤区一模 题型：解答题

    已知：函数f(x)=
    x
    ax+b
    (a，b∈R，ab≠0)    ，f(2)=
    2
    3
    ，f(x)=x    有唯一的根．
    （1）求a，b的值；
    （2）数列{an}对n≥2，n∈N总有an=f（an-1），a1=1；求出数列{an}的通项公式．
    （3）是否存在这样的数列{bn}满足：{bn}为{an}的子数列（即{bn}中的每一项都是{an}的项）且{bn}为无穷等比数列，它的各项和为
    1
    2
    ．若存在，找出所有符合条件的数列{bn}，写出它的通项公式，并说明理由；若不存在，也需说明理由．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    （2007•奉贤区一模）已知：函数f(x)=
    x
    ax+b
    (a，b∈R，ab≠0)    ，f(2)=
    2
    3
    ，f(x)=x    有唯一的根．
    （1）求a，b的值；
    （2）数列{an}对n≥2，n∈N总有an=f（an-1），a1=1；求出数列{an}的通项公式．
    （3）是否存在这样的数列{bn}满足：{bn}为{an}的子数列（即{bn}中的每一项都是{an}的项）且{bn}为无穷等比数列，它的各项和为
    1
    2
    ．若存在，找出所有符合条件的数列{bn}，写出它的通项公式，并说明理由；若不存在，也需说明理由．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    （2007•奉贤区一模）已知：函数f(x)=
    x
    ax+b
    (a，b∈R，ab≠0)    ，f(2)=
    2
    3
    ，f(x)=x    有唯一的根．
    （1）求a，b的值；
    （2）数列{an}对n≥2，n∈N总有an=f（an-1），a1=1；求证{
    1
    an
    }    为等差数列，并求出{an}的通项公式．
    （3）是否存在这样的数列{bn}满足：{bn}为{an}的子数列（即{bn}中的每一项都是{an}的项）且{bn}为无穷等比数列，它的各项和为
    1
    2
    ．若存在，找出一个符合条件的数列{bn}，写出它的通项公式；若不存在，说明理由．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    1.如果一个数列从第　　　　　　项起，每一项与前一项的　　　　　等于同一个常数，那么这个数列就叫做等比数列.这个常数叫做等比数列的　　　　　　　　　，通常用字母　　　　　表示.

    2.如果a、G、b成等比数列，那么G叫做a与b的　　　，且G＝　　　　　(ab＞0).

    3.等比数列的通项公式为an=　　　　　.

    4.等比数列的前n项和公式为Sn=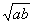

    5.对于正整数m,n,p,q,若m+n=p+q,则等比数列中am,an,ap,aq的关系为　　　　　.

    6.若Sn为等比数列的前n项和，则Sk,S2k-S k,S3k-S2k,…,S(m+1)k-Smk,…成　　　　数列(k＞1且k∈N*).

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    以下命题：
    ①对于任意向量
    a
    、
    b
    ，都有|
    a
    •
    b
    |≥
    a
    •
    b
    成立；
    ②若首项a1＜0，S9=S14，则前n项和Sn取得最小值时n值为11；
    ③已知a，b，b+a成等差数列，a，b，ab成等比数列，且
    1
    2
    ＜logm（a+b）＜1，则实数m的取值范围是（6，36）；
    ④在锐角三角形ABC中，若A=2B，则
    b
    a
    的取值范围是（
    		2
    ，
    		3
    ），
    其中正确命题是
    ①③
    ①③
    （填正确命题的番号）

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    下面有5个命题：
    ①数列{an}是等差数列的充要条件是an=pn+q（p≠0）
    ②如果一个数列{an}的前n项和Sn=abn+c（a≠0，b≠0，b≠1），则此数列是等比数列的充要条件是a+c=0
    ③若命题p的逆命题是q，命题p的否命题是r，则q是r的逆否命题；
    ④函数f（x）=ax2+bx+3a+b是偶函数，其定义域为[a-1，2a]，则f(x)在(-
    2
    3
    ，-
    1
    3
    )    上是减函数；
    ⑤向量
    AB
    =(3，4)按向量
    a
    =(1，2)    平移后为（2，2）
    其中真命题的编号是
    ②③④
    ②③④
    （写出所有真命题的编号）

    查看答案和解析>>

    科目：高中数学 来源：高三数学教学与测试 题型：044

    平移抛物线y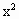＝，使它的顶点在右半平面内沿着抛物线y＝(a为正常数)滑动(如图)，(1)证明：无论抛物线平移到什么位置，它与x轴负半轴的交点A是定点，而与x轴正半轴的交点B，与y轴交点C的连线BC的斜率为定值；(2)线段AB被y轴分成两部分，当其中较大部分长度是|AB|和较小部分长度的等比中项时，求△ABC的面积．

    查看答案和解析>>


    同步练习册答案