设{|an|}(n∈N*)是递增的等比数列,对于给定的k(k∈N*),若 ,则数列{an}(n=1,2,3,…,k)的个数为 ,则数列{an}(n=1,2,3,…,k)的个数为 |
A.2个
B.4个
C.2k个
D.无穷多个 |
相关习题
科目:高中数学
来源:2011年河北省衡水市冀州中学高考数学一模试卷(理科)(解析版)
题型:选择题
设{|a
n|}(n∈N
*)是递增的等比数列,对于给定的k(k∈N
*),若

,则数列{a
n}(n=1,2,3,…,k)的个数为( )
A.2个
B.4个
C.2
k个
D.无穷多个
查看答案和解析>>
科目:高中数学
来源:2011年上海市闵行区高考数学一模试卷(理科)(解析版)
题型:选择题
设{|a
n|}(n∈N
*)是递增的等比数列,对于给定的k(k∈N
*),若

,则数列{a
n}(n=1,2,3,…,k)的个数为( )
A.2个
B.4个
C.2
k个
D.无穷多个
查看答案和解析>>
科目:高中数学
来源:
题型:单选题
设{|an|}(n∈N*)是递增的等比数列,对于给定的k(k∈N*),若 ,则数列{an}(n=1,2,3,…,k)的个数为
,则数列{an}(n=1,2,3,…,k)的个数为
- A.
2个
- B.
4个
- C.
2k个
- D.
无穷多个
查看答案和解析>>
科目:高中数学
来源:0103 模拟题
题型:单选题
设{|a
n|}(n∈N*)是递增的等比数列,对于给定的k(k∈N*),若
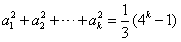
,则数列{a
n}(n=1,2,3,…,k)的个数为
查看答案和解析>>
科目:高中数学
来源:
题型:
已知递增的等比数列{an}的前三项之积是64,且a2-1,a3-3,a4-9成等差数列.
(1)求数列{an}的通项公式an;
(2)设bn=n•an,求数列{bn}的前n项和Sn.
查看答案和解析>>
科目:高中数学
来源:
题型:解答题
已知递增的等比数列{an}的前三项之积是64,且a2-1,a3-3,a4-9成等差数列.
(1)求数列{an}的通项公式an;
(2)设bn=n•an,求数列{bn}的前n项和Sn.
查看答案和解析>>
科目:高中数学
来源:不详
题型:解答题
已知递增的等比数列{an}的前三项之积是64,且a2-1,a3-3,a4-9成等差数列.
(1)求数列{an}的通项公式an;
(2)设bn=n•an,求数列{bn}的前n项和Sn.
查看答案和解析>>
科目:高中数学
来源:2007-2008学年浙江省宁波市高一(下)期末数学试卷(解析版)
题型:解答题
已知递增的等比数列{an}的前三项之积是64,且a2-1,a3-3,a4-9成等差数列.
(1)求数列{an}的通项公式an;
(2)设bn=n•an,求数列{bn}的前n项和Sn.
查看答案和解析>>
科目:高中数学
来源:不详
题型:解答题
已知递增的等比数列{a
n}满足:a
2+a
3+a
4=28,a
3+2是a
2与a
4的等差中项.
(1)求数列{a
n}的通项公式;
(2)假设b
n=
,其数列{b
n}的前n项和T
n,并解不等式T
n<
.
查看答案和解析>>
科目:高中数学
来源:
题型:
等比数列{a
n}的各项均为正数,且2a
1+3a
2=1,a
32=9a
2a
6(1)求数列{a
n}的通项公式.
(2)求数列{
}的前n项和S
n;
(3)设 b
n=log
a
3+…+log
a
2n-1(n∈N
*),若数列{b
n+kn)是递增的数列,求k的取值范围..
查看答案和解析>>

 ,则数列{an}(n=1,2,3,…,k)的个数为
,则数列{an}(n=1,2,3,…,k)的个数为  ,则数列{an}(n=1,2,3,…,k)的个数为( )
,则数列{an}(n=1,2,3,…,k)的个数为( ) ,则数列{an}(n=1,2,3,…,k)的个数为( )
,则数列{an}(n=1,2,3,…,k)的个数为( ) ,则数列{an}(n=1,2,3,…,k)的个数为
,则数列{an}(n=1,2,3,…,k)的个数为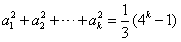 ,则数列{an}(n=1,2,3,…,k)的个数为
,则数列{an}(n=1,2,3,…,k)的个数为