练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    若向量a在y轴上的坐标为0，其他坐标不为0，那么与向量a平行的坐标平面是

    A．xOy平面
    B．xOz平面
    C．yOz平面
    D．以上都有可能
    B
    请在这里输入关键词：
    相关习题

    科目：高中数学 来源： 题型：

    若向量
    a
    在y轴上的坐标为0，其他坐标不为0，那么与向量
    a
    平行的坐标平面是（　　）
    A、xOy平面
    B、xOz平面
    C、yOz平面
    D、以上都有可能

    查看答案和解析>>

    科目：高中数学 来源：同步题 题型：单选题

    若向量a在y轴上的坐标为0，其他坐标不为0，那么与向量a平行的坐标平面是
    [     ]
    A．xOy平面
    B．xOz平面
    C．yOz平面
    D．以上都有可能

    查看答案和解析>>

    科目：高中数学 来源： 题型：

     若向量a在y轴上的坐标为0，其他坐标不为0，那么与向量a平行的坐标平面是

    A. xOy平面      B. xOz平面      C. yOz平面      D. 以上都有可能

    查看答案和解析>>

    科目：高中数学 来源：数学教研室 题型：013

    若向量a在y轴上的坐标为0，其他坐标不为0，那么与向量a平行的坐标平面是

    [　　]

    A．xOy平面
    B．xOz平面
    C．yOz平面
    D．以上都有可能

    查看答案和解析>>

    科目：高中数学 来源： 题型：013

    若向量a在y轴上的坐标为0，其他坐标不为0，那么与向量a平行的坐标平面是

    [　　]

    A．xOy平面

    B．xOz平面

    C．yOz平面

    D．以上都有可能

    查看答案和解析>>

    科目：高中数学 来源：《4.3 空间直角坐标系》2010年同步练习（解析版） 题型：选择题

    若向量在y轴上的坐标为0，其他坐标不为0，那么与向量平行的坐标平面是（ ）
    A．xOy平面
    B．xOz平面
    C．yOz平面
    D．以上都有可能

    查看答案和解析>>

    科目：高中数学 来源： 题型：单选题

    若向量数学公式在y轴上的坐标为0，其他坐标不为0，那么与向量数学公式平行的坐标平面是


    1. A.
      xOy平面
    2. B.
      xOz平面
    3. C.
      yOz平面
    4. D.
      以上都有可能

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    在空间直角坐标系O-xyz中，
    OP
    =x
    i
    +y
    j
    +z
    k
    （其中
    i
    ，
    j
    ，
    k
    分别为x轴、y轴、z轴正方向上的单位向量）．有下列命题：
    ①若
    OP
    =x
    i
    +y
    j
    +0
    k
    (x＞0，y＞0)    且|
    OP
    -4
    j
    |=|
    OP
    +2
    i
    |    ，则
    1
    x
    +
    2
    y
    的最小值为2
    		2

    ②若
    OP
    =0
    i
    +y
    j
    +z
    k
    ，
    OQ
    =0
    i
    +y1
    j
    +
    k
    ，若向量
    PQ
    与
    k
    共线且|
    PQ
    |=|
    OP
    |，则动点P的轨迹是抛物线；
    ③若
    OM
    =a
    i
    +0
    j
    +0
    k
    ，
    OQ
    =0
    i
    +b
    j
    +0
    k
    ，
    OR
    =0
    i
    +0
    j
    +c
    k
    (abc≠0)    ，则平面MQR内的任意一点A（x，y，z）的坐标必须满足关系式
    x
    a
    +
    y
    b
    +
    z
    c
    =1；
    ④设
    OP
    =x
    i
    +y
    j
    +0
    k
    (x∈[0，4]，y∈[-4，4])    ，
    OM
    =0
    i
    +y1
    j
    +
    k
    (y1∈[-4，4])    ，
    ON
    =x2
    i
    +0
    j
    +0
    k
    (x2∈[0，4])    ，若向量
    PM
    ⊥
    j
    ，
    PN
    与
    j
    共线且|
    PM
    |=|
    PN
    |，则动点P的轨迹是双曲线的一部分．
    其中你认为正确的所有命题的序号为
    ②③④
    ②③④
    ．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    （2013•安庆三模）已知焦点在x轴上的椭圆C1：
    x2
    a2
    +
    y2
    12
    =1和双曲线C2：
    x2
    m2
    -
    y2
    n2
    =1的离心率互为倒数，它们在第一象限交点的坐标为（
    4
    		10
    5
    ，
    6
    		5
    5
    ），设直线l：y=kx+m（其中k，m为整数）．
    （1）试求椭圆C1和双曲线C2 的标准方程；
    （2）若直线l与椭圆C1交于不同两点A、B，与双曲线C2交于不同两点C、D，问是否存在直线l，使得向量
    AC
    +
    BD
    =
    0
    ，若存在，指出这样的直线有多少条？若不存在，请说明理由．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

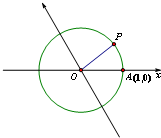    定义：平面内两条相交但不垂直的数轴构成的坐标系（两条数轴的原点重合且单位长度相同）称为平面斜坐标系；在平面斜坐标系xOy中，若
    OP
    =x
    e1
    +y
    e2
    （其中
    e1
    、
    e2
    分别是斜坐标系x轴、y轴正方向上的单位向量，x、y∈R，O为坐标原点），则有序实数对（x，y）称为点P的斜坐标．在平面斜坐标系xOy中，若∠xOy=120°，点A（1，0），P为单位圆上一点，且∠AOP=θ，点P在平面斜坐标系中的坐标是（　　）

    查看答案和解析>>


    同步练习册答案