
| 若一个命题的结论是 “直线l在平面α内”,则用反证法证明这个命题时,第一步应假设为 |
A.假设直线l∥平面α B.假设直线l∩平面α于点A C.假设直线l  平面α 平面α D.假设直线l⊥平面α |
科目:高中数学 来源:北京期中题 题型:单选题
[ ]
 平面α
平面α 科目:高中数学 来源: 题型:013
[ ]
A. 0 B. 1 C. 2 D. 3
科目:高中数学 来源: 题型:
| OP |
| OA1 |
| OA2 |
| OP |
| OA1 |
| OA2 |
| OAn |
| OP |
| OA1 |
| OA2 |
| OAn |
| OP |
| OA1 |
| OA2 |
| OAn |
科目:高中数学 来源: 题型:解答题
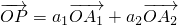 ,求a1+a2的值;
,求a1+a2的值;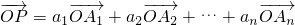 ,我们称
,我们称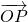 是向量
是向量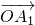 ,
,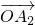 ,…,
,…,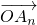 的线性组合,{an}是该线性组合的系数数列.当
的线性组合,{an}是该线性组合的系数数列.当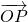 是向量
是向量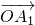 ,
,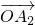 ,…,
,…,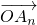 的线性组合时,请参考以下线索:
的线性组合时,请参考以下线索:科目:高中数学 来源:2011年上海市普陀区高考数学一模试卷(理科)(解析版) 题型:解答题
 ,求a1+a2的值;
,求a1+a2的值; ,我们称
,我们称 是向量
是向量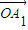 ,
,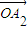 ,…,
,…, 的线性组合,{an}是该线性组合的系数数列.当
的线性组合,{an}是该线性组合的系数数列.当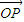 是向量
是向量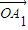 ,
, ,…,
,…, 的线性组合时,请参考以下线索:
的线性组合时,请参考以下线索:科目:高中数学 来源:不详 题型:填空题
科目:高中数学 来源: 题型:022
设α、β表示平面,l表示不在α内也不在β内的直线,存在下列三个事实:
①l⊥α;②l∥β;③α⊥β,若以其中两个作为条件,另一个作为结论,可构成三个命题,其中真命题是_________.(要求写出所有真命题)
科目:高中数学 来源:数学教研室 题型:022
①l⊥α;②l∥β;③α⊥β,若以其中两个作为条件,另一个作为结论,可构成三个命题,其中真命题是_________.(要求写出所有真命题)
科目:高中数学 来源: 题型:
科目:高中数学 来源:不详 题型:填空题
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com